PBD - Position Based Dynamics

不同于传统意义的PBA（即 Physically based Animation），PBD ¹ 并不是传统意义上基于物理的模拟，但能够提供视觉上可信且计算效率极高的模拟效果，故而常用于在对于realtime要求比较高的情景下，比如电子游戏

物理模型

物理对象

物理对象包括如下几种：

• Actor - Static ：静态的物体阻挡
• Actor - Dynamic ：符合动力学原理的 Actor，可以移动的物体
• Trigger：触发器
• Actor - Kinematic：特殊的 Dynamic actor，根据游戏需要的运动物体，不符合动力学原理的 Actor

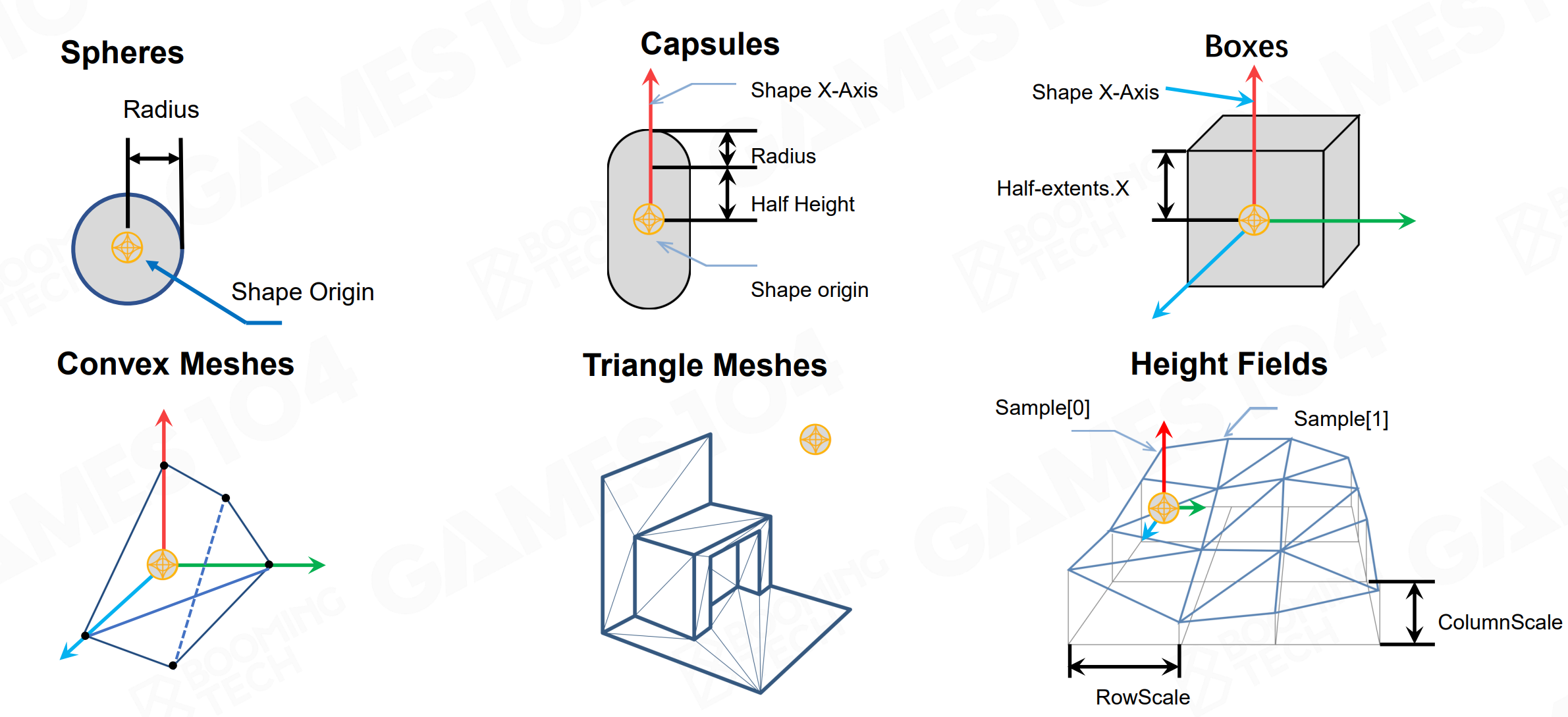
Actor 形状

物理中 Actor 形状又如下几种

• Sphere：球体
• Capsules：胶囊体
• Boxes：长方体/立方体
• Convex Meshes：凸包/凸多面体
• Triangle Meshes：
• Height Fields：高度场

力

持续的力

• Gravity：重力
• Drag：拉力
• Friction： 摩擦力

瞬时力

• Impulse：冲力（爆炸或者碰撞产生的力）

运动

牛顿第一定律

匀速运动：

没有外力的作用下速度保持不变：

$$\begin{aligned}
\vec{v}(t + \Delta t) = \vec{v}(t) & \leftarrow \vec{v_t} = \vec{v_0} \
\vec{x}(t + \Delta t) = \vec{x}(t) + \vec{v}(t) \Delta t & \leftarrow \vec{x_t} = \vec{x_0} + \vec{v_t}t
\end{aligned}$$

牛顿第二定律

当有外力的情况下：

$$\begin{aligned}
\vec{F} & = m \vec{a} \
\vec{a}(t) & = \frac{d \vec{v}(t) }{ dt } = \frac{ d^2\vec{x}(t) }{ dt^2 } \leftarrow \vec{a} = \frac{v}{t}=\frac{x}{t^2}
\end{aligned}$$

外力恒定不变（大小，方向）的情况下：

$$\begin{aligned}
\vec{v}(t + \Delta t) & = \vec{v}(t) + \vec{a}(t) \Delta t \
\vec{x}(t + \Delta t) & = \vec{x}(t) + \vec{v}(t) \Delta t + \frac{1}{2}\vec{a}(t) \Delta t^2
\end{aligned}$$

当外力变化的情况（因为加速度是变化的，速度计算是在这段时间内对加速度跟时间求积分）：

$$\begin{aligned}
\vec{v}(t + \Delta t) = \vec{v}(t) + \int_{t}^{t + \Delta t}{ \vec{a}(t’) dt’ } \
\vec{x}(t + \Delta t) = \vec{x}(t) + \int_{t}^{t + \Delta t}{ \vec{v}(t’) dt’ }
\end{aligned} $$

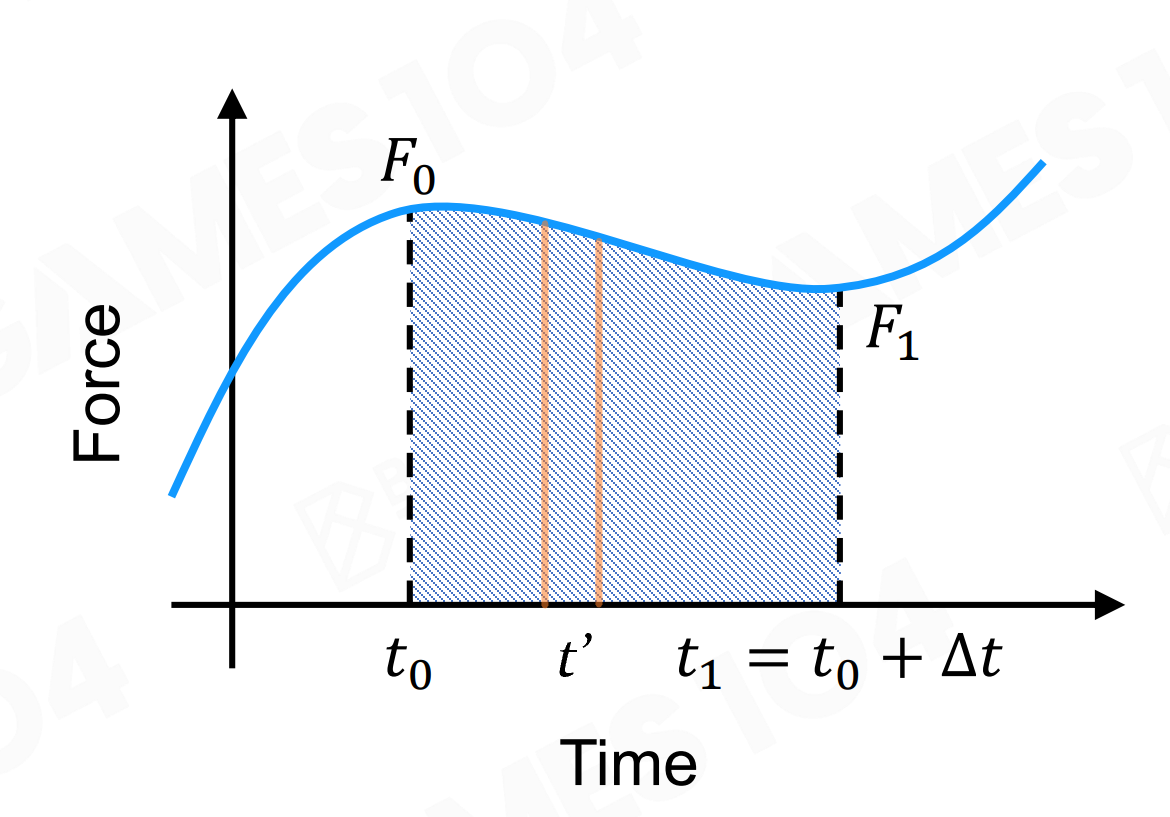
物理模拟求解问题

应用到游戏中，就是我们已知 $t$ 时刻的物体的信息如下：

• $\vec{x}(t)$：位置
• $\vec{v_t} = \frac{d\vec{x}(t)}{dt}$：速度
• $m$：质量

求解下一个时刻 $\Delta t$ 的位置 $\vec{x}(t + \Delta t)$ 跟 速度 $\vec{v}_{t+\Delta t}$

$\Delta t$ 是模拟步长时间，游戏帧率是 30 帧，则 $\Delta t = \frac{1}{30}$秒）的位置跟速度。

欧拉方法

显示欧拉法：Explicit（Forward）Euler’s Method

最简单直观的模拟方法，假设力不变的情况下，我们可以通过受力分析，得到加速度，直接求出下一个时刻的速度跟位置：

$$\begin{aligned}
\vec{v}(t_1) &= \vec{v}(t_0) + M^{-1} \vec{F}(t_0) \Delta t \
\vec{x}(t_1) &=\vec{x}(t_0) + \vec{v}(t_0) \Delta t
\end{aligned}$$

1. 下一个时刻的速度 $\vec{v}(t_1)$ 等于当前时刻的速度 $\vec{v}(t_0)$ 加上当前时刻的加速度 $M^{-1} \vec{F}(t_0)$ 乘上 $\Delta t$
2. 下一个时刻的位置 $\vec{x}(t_1)$ 等于当前时刻的位置 $\vec{x}(t_1)$，加上在 $\Delta t$ 时间的位移 $\vec{v}(t_0) \Delta t$

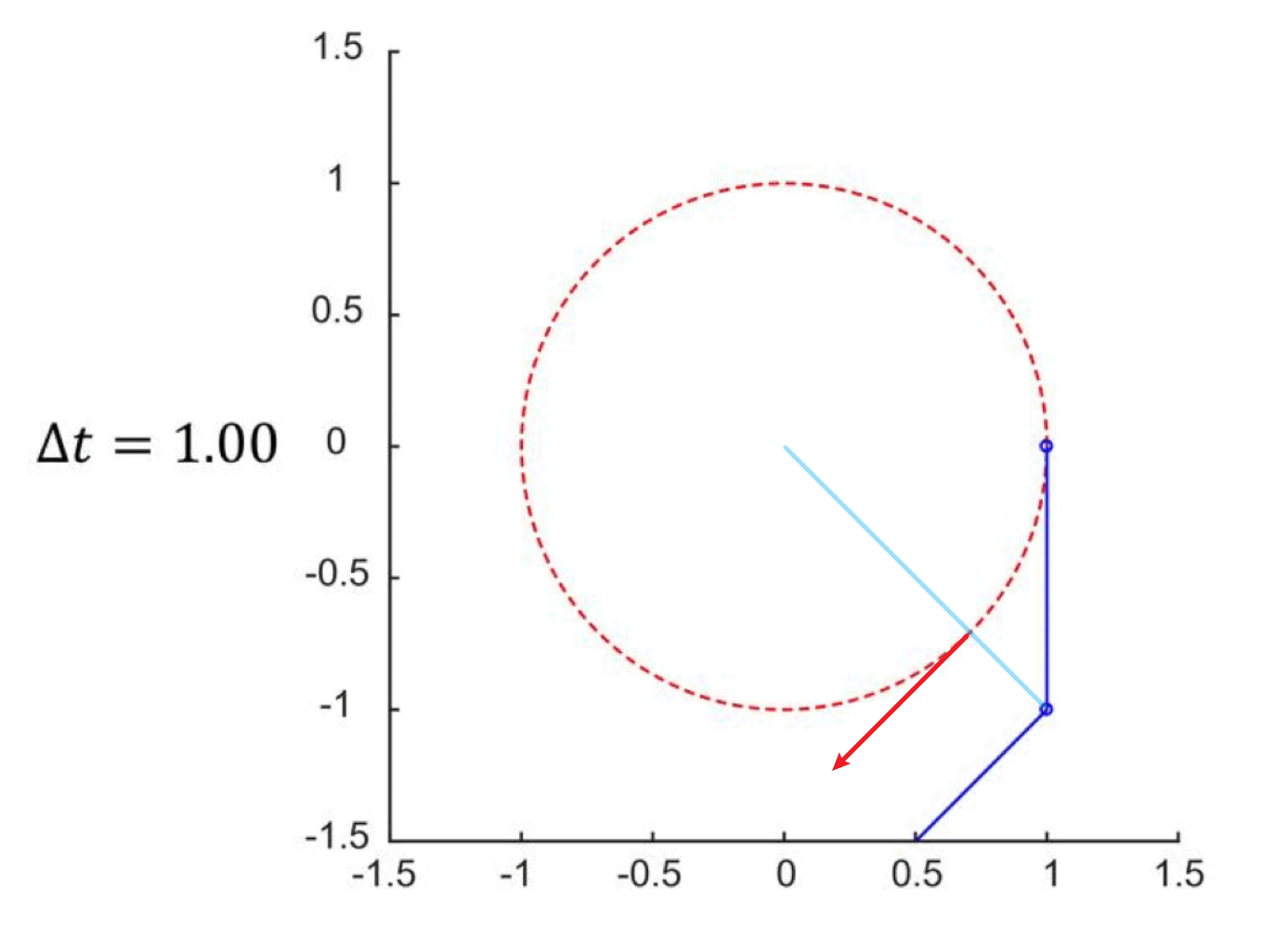
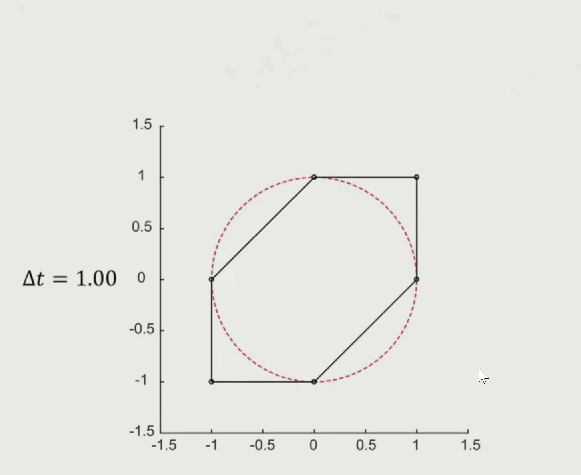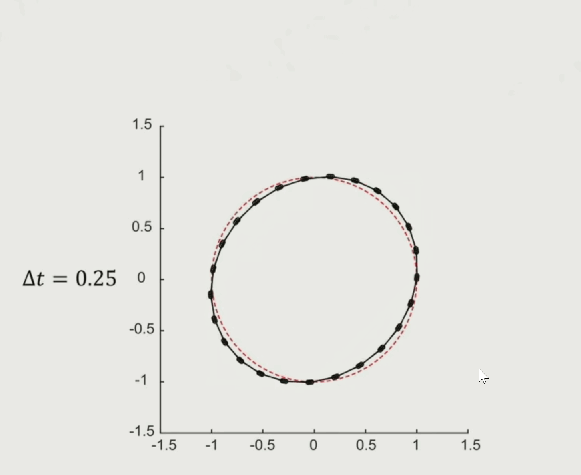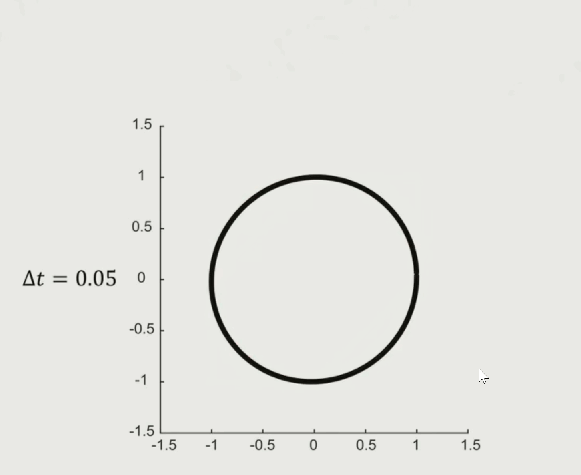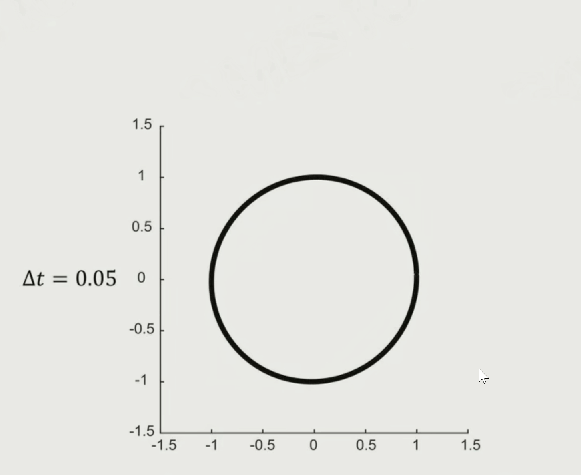
缺点：不收敛，如下图，蓝色线是模拟的运动轨迹，红色箭头是我们希望得到的收敛轨迹，从运动轨迹上看，随着时间的推移，运动会越来越偏离红色圈的预期轨道，不满足能量守恒，能量会随着模拟进行慢慢膨胀。

随着模拟时间步长减小，模拟轨迹越来越接近预期轨道，但还是发散的（只看结论）

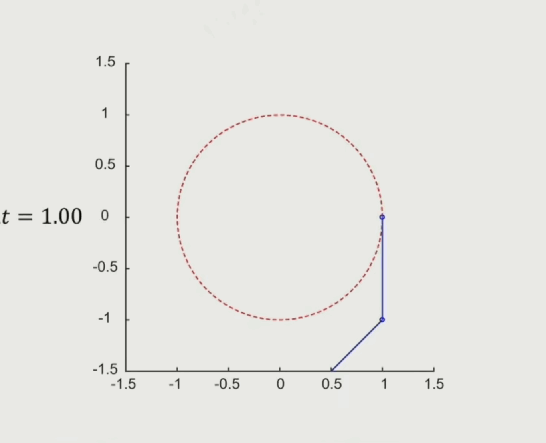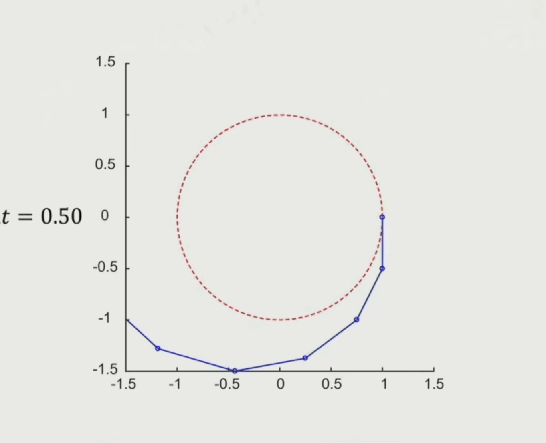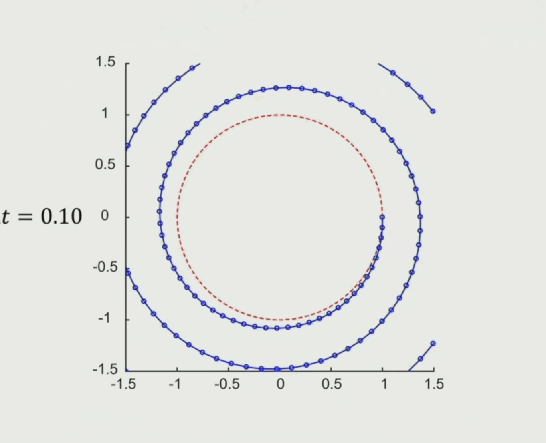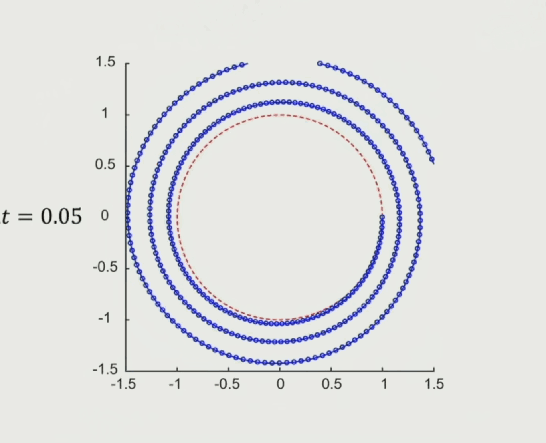
隐式欧拉法：Implicit（Backward）Euler’s Method

显示欧拉法使用的是当前时刻的加速度跟速度来模拟下一个时刻的速度跟位置，隐式欧拉则是通过对下一个时刻进行受力分析，计算加速度跟速度来模拟下一个时刻的位置：

$$\begin{aligned}
\vec{v}(t_1) &= \vec{v}(t_0) + M^{-1} \textcolor{Red}{\vec{F}(t_1) } \Delta t \
\vec{x}(t_1) &=\vec{x}(t_0) + \textcolor{Red}{ \vec{v}(t_1) } \Delta t
\end{aligned}$$

如果未来时刻的受力跟位置有关系的话，计算就非常难，隐式欧拉法的好处是系统的能量是衰减的，符合真实的物理模拟中，有摩擦力、空气阻力的情况。

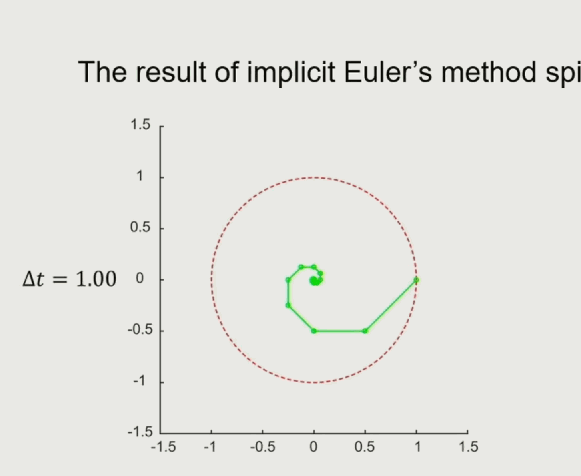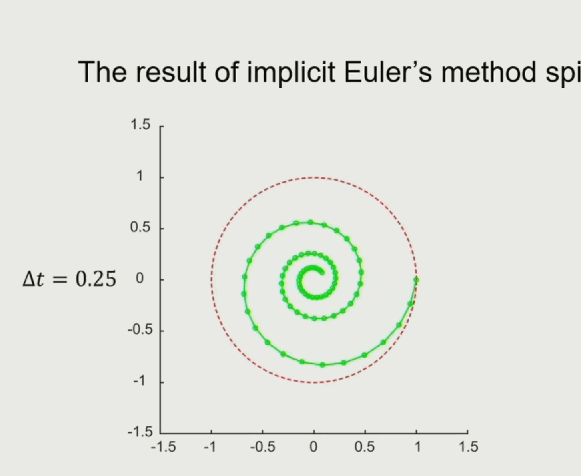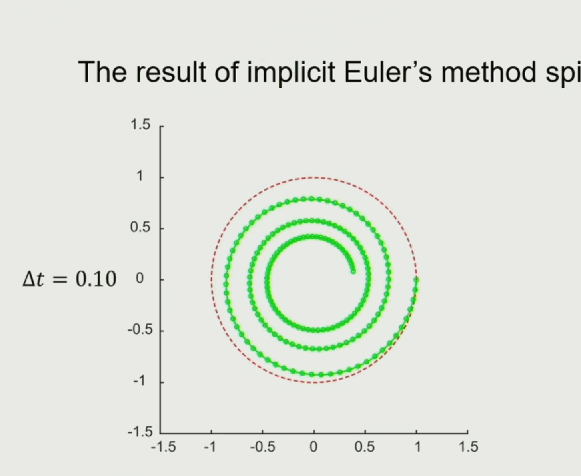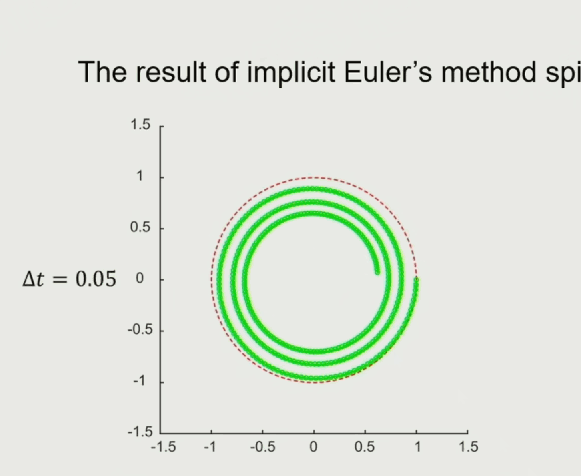
半隐式欧拉法（Semi-implicit Euler’s Method)

结合了显示欧拉法跟半隐式欧拉法的方法，假设力不会随着位置变化而变化（其实真实情况会变化）：

$$\begin{aligned}
\vec{v}(t_1) &= \vec{v}(t_0) + M^{-1} \textcolor{SkyBlue}{\vec{F}(t_0) } \Delta t \
\vec{x}(t_1) &=\vec{x}(t_0) + \textcolor{Red}{ \vec{v}(t_1) } \Delta t
\end{aligned}$$

1. 用当前时刻的受力分析，计算下一个时刻的速度 $\vec{v}(t_1)$
2. 用估计得到的下一时刻的速度 $\vec{x}(t_1)$ 来计算下一个时刻的位置

刚体动力学（Rigid Body Dynamics）

例子动力学（Particle Dynamics）

物理变量	数学表达
Position： 位置	$\vec{x}$
Linear Velocity：速度	$\vec{v} = \frac{d\vec{x}}{dt}$
Acceleration：加速度	$\vec{a} = \frac{d\vec{v}}{dt}= \frac{d2{\vec{x}}}{dt2}$
Mass：质量	M
Momentum：动量	$\vec{p}=M\vec{v}$
Force：冲力	$\vec{F}=\frac{d \vec{p} }{dt} = M \vec{a}$

Linear Velocity：区别于后面的角速度

Rigid Body Dynamics

区别于质点模型，刚体有旋转量。

物理变量	数学表达
Orientation：姿态	$ \boldsymbol R $
Angular Velocity：角速度	$\vec{w} = \frac{\vec{v} \times \vec{r} }{ | \vec{v} | }$
Angular Acceleration：角加速度	$\vec{\alpha} = \frac{ d\vec{w} }{ dt } = \frac{ \vec{a} \times \vec{r} }{ | \vec{r} | ^2 }$
Inertia tensor：转动惯量（转动惯量张量）	$ \boldsymbol I = \boldsymbol R \cdot \boldsymbol I_0 \cdot \boldsymbol R^T$
Angular Momentum：角动量	$\vec{L}= I \vec{w}$
Torque：力距	$\vec{\tau} = \frac{ d \vec{L} }{ dt }$

经典牛顿力学应用

这里举个使用经典力学做布料模拟的例子 ³，下面是一个布料系统的建模 ⁴，思路是将一块布料视作由一个个质点构成的网格，网格之间由弹簧相连接，如下图：

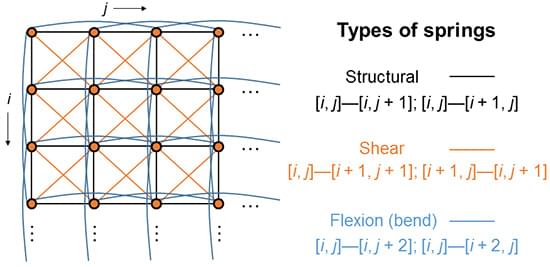
质点之间的连接分为三种，分别用来模拟材料的三种力：

• 上下左右相邻质点连接（黑色线条），模拟结构力（Structural），拉伸跟收缩力。
• 对角线连接（橙色线条），模拟剪力（Shear）
• 上下左右跨一个质点连接，用来模拟材料弯曲的力（Flexion）

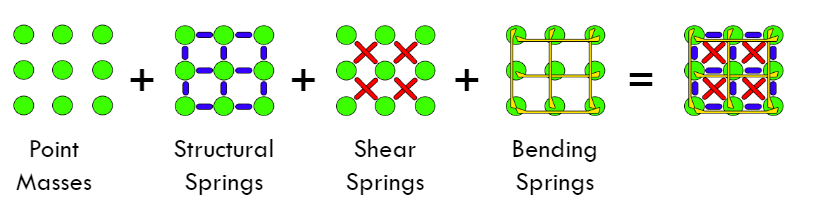
弹力

质点内部弹簧力：$F_i = F_{structural} + F_{shear} + F_{flexion}$，弹力满足胡克定律：

$$
F=-K_s \Delta x
$$

$\Delta x $ 为弹簧的伸缩量

阻尼力

质点在运动的时候，通常是有能量损耗的，如果没有损耗，弹簧振子就会永远震动下去，这不符合实际情况，因此加入阻尼力来模拟这种损耗：

$$
F_d = -C_dv
$$

其中 $C_d$ 为阻尼系数， $v$ 为运动方向

重力

布料质点的重力公式：

$$
F_g = mg
$$

质点的质量 $m$ 可以将布料的总质量 $M$ 除以质点个数得到

外力

布料还会受到一些外力，例如风力等，记为 $F_e$

运动方程

综合上面的受力，我们就能得到质点的合力方程：$F=F_i + F_d + F_d + F_g + F_e$，然后使用之前提到的半隐式欧拉公式：

$$\begin{aligned}
\vec{v}(t_1) &= \vec{v}(t_0) + M^{-1} \textcolor{SkyBlue}{\vec{F}(t_0) } \Delta t \
\vec{x}(t_1) &=\vec{x}(t_0) + \textcolor{Red}{ \vec{v}(t_1) } \Delta t
\end{aligned}$$

重复以上步骤，即可以模拟布料运动了。

代码分析

参数定义

使用两个 Buffer，分别来存储质点的位置跟速度，使用线程数组存储二维质点：

// 所有质点的位置
RWStructuredBuffer<float4> positions;
// 所有质点的速度
RWStructuredBuffer<float3> velocities;

// size 是质点个数
static uint getIndex(uint2 id){
    return id.y * size.x + id.x;
}

下面是计算过程中会使用到的参数：

// x 表示横向质点数量，y 表示纵向质点数量  z = x * y
uint4 size;

// 弹性系数（胡克定律）, xyz 分别对应结构弹簧、剪力弹簧、弯曲弹簧
float3 springKs;

// 弹簧在松弛状态下的长度（初始长度），xyz 分别对应结构弹簧、剪力弹簧、弯曲弹簧
uniform float3 restLengths;

// 单个质点的质量
uniform float mass;

// 阻尼系数
#define Cd 0.5

// 流体(风)参数
float4 viscousFluidArgs;
#define Uf viscousFluidArgs.xyz
#define Cv viscousFluidArgs.w

// 单次迭代时间间隔
float deltaTime;
#define dt deltaTime


// 宏定义
#define totalParticleCount size.z
#define L0 restLengths.x
#define M mass

运行流程大致是：

// 初始化质点
Init();

while(true)
{
    // 计算速度
    StepV();

    // 计算位置
    StepP();
}

初始化代码：

void Init (uint3 id : SV_DispatchThreadID)
{
    uint index = getIndex(id.xy);
    positions[index] = float4(id.x * L0, 0, id.y * L0, 0);
    velocities[index] = float3(0, 0, 0);
    normals[index] = float4(0, 1, 0, 0);
}

然后计算速度时，进行受力分析：

void StepV (uint3 id : SV_DispatchThreadID)
{
    stepVelocity(id.xy);
}

static void stepVelocity(uint2 id)
{
    uint index = getIndex(id);
    // 计算合力
    float3 f = calculateF(id);

    // 计算加速度 F * M^(-1)
    float3 a = f * rcp(M);

    // 计算速度
    float3 velocity = getVelocity(index);
    velocity = velocity + a * dt;

    // 更新速度
    velocities[index] = velocity;
    updateNormal(id);
}

static float3 calculateF(uint2 id, float3 position, float3 velocity)
{
    uint index = getIndex(id);
    float3 f = float3(0, 0, 0);
    // 弹性力求和
    f = calcTotalSpring(id, position)

    // 阻尼力
    float3 fd = - Cd * velocity;
    f += fd;

    // 重力
    float3 fg = float3(0, -9.8, 0) * M;
    f += fg;

    // 模拟风力
    float3 normal = getNormal(index);
    float3 fv = Cv * (dot(normal, Uf - velocity)) * normal;
    f += fv;

    return f;
}

其中弹力计算：根据胡克定律，当我们知道两个质点的位置以及它们的弹性系数，就可以计算出质点的受力：

//结构弹簧的4个方向
static uint2 SpringDirs[12] = 
{
    //结构力
    {1,0},
    {0,1},
    {-1,0},
    {0,-1},
    //剪力
    {-1,-1},
    {-1,1},
    {1,-1},
    {1,1},
    //弯矩力
    {-2,0},
    {2,0},
    {0,2},
    {0,-2},
};

static bool isValidateId(uint2 id)
{
    return id.x >= 0 && id.x < size.x && id.y >= 0 && id.y < size.y;
}

static float3 calcTotalSpring(uint2 id, float3 position)
{
    float3 f = float3(0, 0, 0);
    for(uint i = 0; i < 12; i ++)
    {
        uint2 nId = id + SpringDirs[i];
        uint nIndex = getIndex(nId);
        if(isValidateId(nId))
        {
            float3 nPos = getPosition(nIndex);
            f += getSpring(position, nPos, i / 4);
        }
    }
    return f;
}

// 弹性力计算
// springType 0, 1, 2 分别代表结构弹簧、剪力弹簧、弯曲弹簧
static float3 getSpring(float3 p, float3 q, uint springType)
{
    float3 dp = p - q;
    float len = length(dp);
    float restL = restLengths[springType];
    // F = -kx
    // k      : springKs[springType]
    // restL  : L0
    // len    : L

    // dp / L : 单位向量
    // F = -k * dp / L * (L - L0)
    return dp * (springKs[springType] * (restL * rcp(len) - 1));
}

最后更新位置：

void StepP (uint3 id : SV_DispatchThreadID)
{
    if(id.y == 0 && (id.x == 0 || id.x == size.x - 1) )
    {
        // pin two corner
        // 固定最左最右两个点
        return;
    }

    stepPosition(id.xy);
}

static void stepPosition(uint2 id)
{
    uint index = getIndex(id);
    float3 velocity = getVelocity(index);
    float3 position = getPosition(index);
    position += velocity * dt;
    setPosition(index,position);

    // 检查是否有碰撞
    detechBallCollision(id);
}

PBD 算法

PBD 算法基本定义

首先定义 节点数据： $i \in [1, …, N]$

• $N$ ：节点个数
• $m_i$：节点的质量
• $x_i$：节点位置
• $v_i$：节点速度

第二部分是 约束数据：$j \in [1, …, M]$

• $M$：$M$ 个约束函数
• $n_j$：基数（约束函数中例子个数）
• $C_j：\mathbb{R}^{3n_j} \rightarrow \mathbb{R}$：约束函数（在三维坐标中，每个节点坐标由 3 个坐标）
• $ {i_1, … , i_{n_j} }, i_k \in [1, … , N]$：约束函数中节点
• $k_j \in [0, 1]$：约束刚度参数
• $C_j(x_{i_1}, … , x_{i_{n_j}}) = 0$：约束等式
• $C_j(x_{i_1}, … , x_{i_{n_j}}) \geq 0$：约束不等式

约束函数可以是等式约束，或者不等式约束

对于一个等式约束 $C(p) = C(p_1, … , p_n) = 0$，对于当前的位置 $p$ 我们需要计算一个 $\Delta p$，使得质点在当前位置移动 $\Delta p$ 后满足约束（$\Delta p $ 为零向量时，当前位置就是满足条件的）。

$$
C(p + \Delta p) \approx C(p) + \nabla_p C(p) \cdot \Delta p = 0
$$

泰勒级数
对于一般的函数，泰勒公式系数依赖函数在一点的各阶导数，在 $a$ 处的展开式如下：
$$
f(a+h) = f(a) + f’(a)h + o(h)
$$
其中 $o(h)$ 是比 $h$ 高阶的无穷小，有些情况下可以忽略不计

由于 $\Delta p$ 在梯度的方向上，我们按照梯度方向设置步长系数 $\lambda$ 去迭代跟逼近目标值（我的理解）

$$
\Delta p = \lambda \nabla_p C(p)
$$

带入之前的公式可得：

$$
C(p) + \nabla_p C(p) \cdot \textcolor{Red}{\lambda \nabla_p C(p)} = 0
$$

$$\begin{aligned}
\lambda &= -\frac{C(p)}{||\nabla_p C(p)||^2} \ \Delta p &= -\frac{C(p)}{||\nabla_p C(p)||^2}\nabla_p C(p)
\end{aligned}$$

距离约束（distance constraint）

考虑两个质点弹簧如下

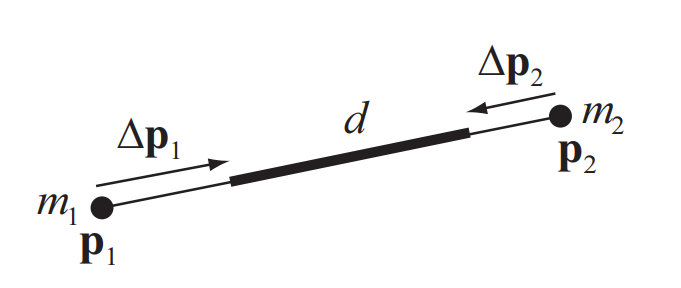
两个质点模型的约束为：两个点之间的距离趋向恒定

$$
C(\vec{x_1}, \vec{x_2}) = ||\vec{x_1} - \vec{x_2}|| - d = 0
$$

在这里 $C(\vec{x_1}, \vec{x_2})$ 是点 $ \boldsymbol p_1$ 跟 $ \boldsymbol p_2$ 一个约束函数，$n_j$ 基数是 2

这里可以直接套用文章中的求解得出 $\Delta p_1$ 和 $\Delta p_2$:

$$\begin{aligned}
\Delta \vec{p_1} &= -\frac{m_2}{m_1 + m_2}(|p_1 - p_2| - d) \frac{p_1 - p_2}{|p_1 - p_2|} \
\Delta \vec{p_1} &= \frac{m_2}{m_1 + m_2}(|p_1 - p_2| - d) \frac{p_1 - p_2}{|p_1 - p_2|}
\end{aligned}$$

弯曲约束

弯曲约束是用来控制相邻两个面片的对折程度，现实中，布料对折时，布料内部结果也存在抵抗弯曲的里。

论文中给出的弯曲约束如下图：

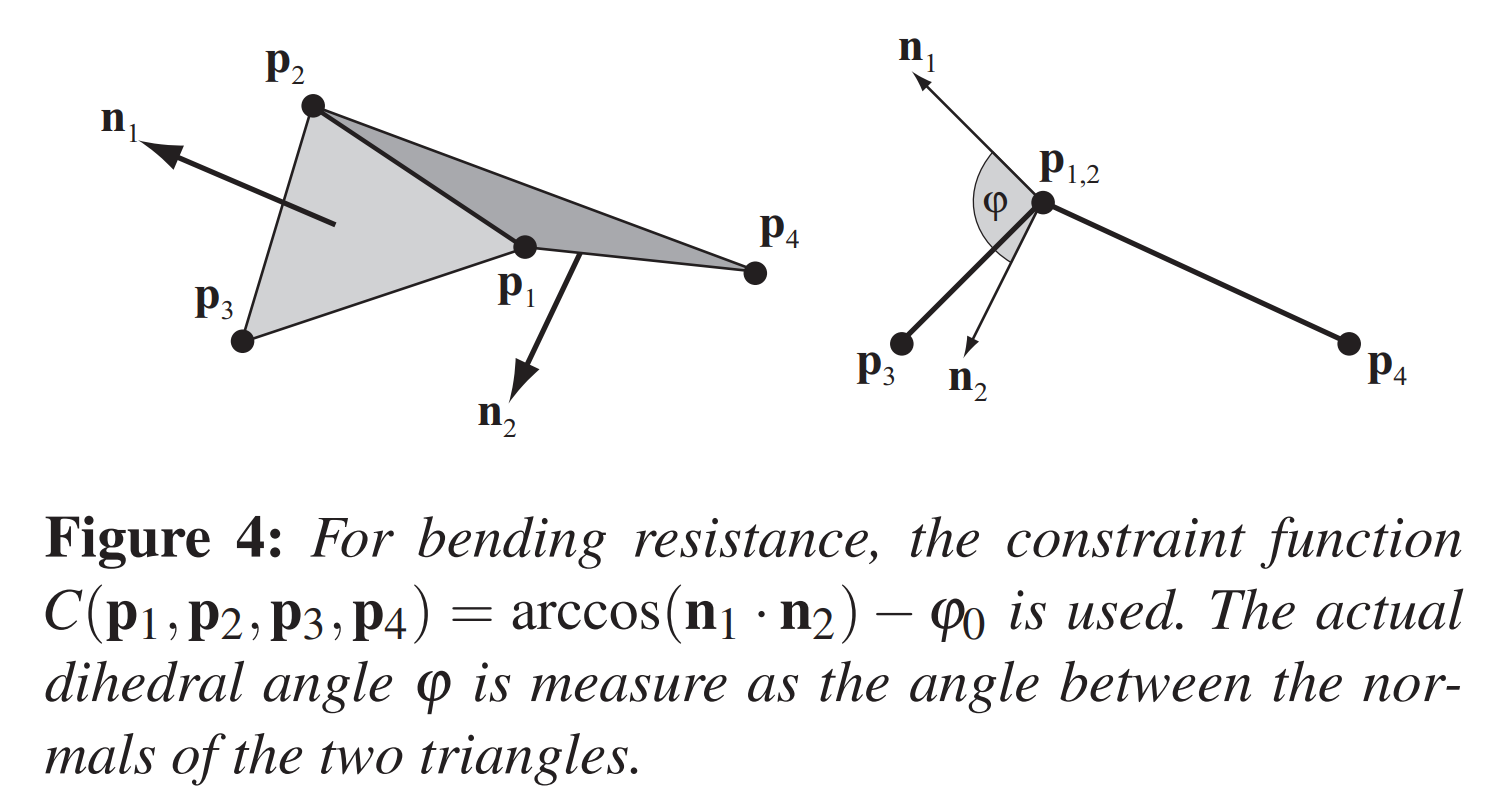
其实就是计算两个相邻的三角面法线之间的夹角，其中包括 4 个顶点，组成一个约束公式：

$$
C_{bend}(p_1, p_2, p_3, p_4)=acos(\frac{(p2 - p1) \times (p3 - p1)}{|(p2 - p1) \times (p3 - p1)|} \cdot \frac{(p2 - p1) \times (p3 - p1)}{|(p2 - p1) \times (p3 - p1)|}) - \varphi_0 = 0
$$

计算结果看论文结论吧：

算法流程

整个算法流程如下图：

首先初始化（step(1) ~ step(3)） $\boldsymbol{x}_i=\boldsymbol{x}_i^{{0}$，$\boldsymbol{v}_i=\boldsymbol{v}_i}0$，$w_i=\frac{1}{m_i}$。然后每个步长 $\Delta t$ 时间内更新一次，计算速度跟位置：

• 处理外力，计算预测速度： $\boldsymbol{v}_i \leftarrow \boldsymbol{v}i+\Delta t w_i \boldsymbol{f}{ext}{\boldsymbol{x}_i}$

1. 这里的 $\boldsymbol{f}_{ext}$ 包含重力，风力等
2. 然后如果有些质点要固定不动，可以将质量设置成无限大，则 $w_i$ 为 0 ，质点的位置就不受影响）

• 处理阻尼： $dampVelocities(\boldsymbol{v}_1, … , \boldsymbol{v}_N)$
• 预测下一个位置：$\boldsymbol{p}_i \leftarrow \boldsymbol{x}_i + \Delta t \boldsymbol{v}_i$

这里也是用到半隐式法

• 碰撞检测，生成 $M_{coll}$ 个碰撞约束： $generateCollisionConstraints(\boldsymbol{x}_i \rightarrow \boldsymbol{p}_i)$
• 若干次迭代：每次迭代处理一遍约束： $projectConstraints(C_1, … , C_{M+M_{coll}}, \boldsymbol{p}_1, …, \boldsymbol{p}_N)$
• 速度、位置更新：$\boldsymbol{v}_i \leftarrow (\boldsymbol{p}_i - \boldsymbol{x}_i)/\Delta t$，$\boldsymbol{x}_i \leftarrow \boldsymbol{p}_i$

代码解析 ^8,10

初始化质量

这里使用的是计算三角面的面积，然后乘以布料的密度，再将质量均摊到三个顶点上。

private void BuildMasses()
{
    _masses = new NativeList<float>(this.vertexCount,Allocator.Persistent);
    _masses.Resize(this.vertexCount,NativeArrayOptions.ClearMemory);
    for(var i = 0; i < indices.Length / 3; i++){
        var offset = i * 3;
        var i0 = indices[offset];
        var i1 = indices[offset + 1];
        var i2 = indices[offset + 2];
        var v0 = vertices[i0];
        var v1 = vertices[i1];
        var v2 = vertices[i2];
        var area = IntersectUtil.GetArea(v0,v1,v2);
        var m = area * _setting.density;
        var m3 = m / 3;
        _masses[i0] += m3;
        _masses[i1] += m3;
        _masses[i2] += m3;
    }
}

初始化完毕后开始迭代步骤

预测速度跟位置

这里只考虑外力（风力跟重力），这里输入数据：

• position - 位置
• velocities - 速度
• normals - 法线
• masses - 质量
• fieldForce - 阻尼系数
• dt - 迭代步长时间

预测公式如下：

$$\begin{aligned}
\vec{v_1} &= \vec{v_0} + (\vec{g} + \frac{\vec{F_e}}{m}) \Delta t \
\vec{v_1} &= \vec{v_1} \cdot max(1-\frac{k_d}{m} \Delta t, 0) \
p_1 &= p_0 + \vec{v_1} \cdot \Delta t
\end{aligned}$$

public void Execute(int index)
{
    var p = positions[index];
    var v = velocities[index];
    var m = masses[index];
    if(m > 0)
    {
        var normal = normals[index];
        var fieldForceAtNormal = math.dot(fieldForce,normal) * normal;
        var v1 = v + ClothSimulator.G * dt + fieldForceAtNormal * dt / m;
        v1 *= math.max(0,(1 - damper * dt / m)); //阻尼
        var p1 = p + v1 * dt;
        predictPositions[index] = p1;
    }
    else
    {
        predictPositions[index] = p;
    }
}

碰撞检测

这里省略

内部约束

使用距离约束跟弯曲约束，来修正之前的预测位置。

var predictPositions = this._predictPositions;
for(var i = 0; i < this.constraintSolverIteratorCount; i ++){
    jobHandle = StartDistanceConstraintsJob(jobHandle,i);
    jobHandle = StartBendConstraintsJob(jobHandle,i);
}

距离约束：

public struct DistanceConstraintJob : IJobFor
{
    public void Execute(int index)
    {
        var constraint = distanceConstriants[index];

        var p0 = predictPositions[constraint.vIndex0];
        var p1 = predictPositions[constraint.vIndex1];
        var m0 = masses[constraint.vIndex0];
        var m1 = masses[constraint.vIndex1];
        var distV = p1 - p0;
        var normal = math.normalize(distV);
        var length = math.length(distV);
        var err = length - constraint.restLength;
        float3 correct;
        if(err < 0){
            correct = compressStiffness * normal * err;
        }else{
            correct = stretchStiffness * normal * err;
        }
        var totalM = m0 + m1;
        positionCorrects[constraint.vIndex0] += correct * di * m1 / totalM;
        positionCorrects[constraint.vIndex1] -= correct * di * m0 / totalM;
    }
}

弯曲约束：

public struct BendConstaintsGenerateJob : IJobFor
{
    public void Execute(int index)
    {
        var cons = bendConstarints[index];
            
        var p1 = predictPositions[cons.vIndex0];
        var p2 = predictPositions[cons.vIndex1] - p1;
        var p3 = predictPositions[cons.vIndex2] - p1;
        var p4 = predictPositions[cons.vIndex3] - p1;
        p1 = 0;
        var n1 = math.normalize(math.cross(p2,p3));
        var n2 = math.normalize(math.cross(p2,p4));

        var d = math.dot(n1,n2);

        var p23Len = math.length(math.cross(p2,p3));
        var p24Len = math.length(math.cross(p2,p4));

        var q3 = (math.cross(p2,n2) + math.cross(n1,p2) * d) / p23Len;
        var q4 = (math.cross(p2,n1) + math.cross(n2,p2) * d) / p24Len;
        var q2 = - (math.cross(p3,n2) + math.cross(n1,p3) * d) / p23Len 
        - (math.cross(p4,n1) + math.cross(n2,p4) * d) / p24Len;
        var q1 = - q2 - q3 - q4;

        var w1 = 1 / masses[cons.vIndex0];
        var w2 = 1 / masses[cons.vIndex1];
        var w3 = 1 / masses[cons.vIndex2];
        var w4 = 1 / masses[cons.vIndex3];

        var sum = w1 * math.lengthsq(q1) 
        + w2 * math.lengthsq(q2) 
        + w3 * math.lengthsq(q3) 
        + w4 * math.lengthsq(q4);

        sum = math.max(0.01f,sum);

        // sqrt(1 - d^2)(acos(d) - varphi0)
        var s = - (math.acos(d) - cons.rest) * math.sqrt(1 - d * d) / sum;

        if(math.isfinite(s)){
            var dp1 = s * w1 * q1 * di * bendStiffness;
            var dp2 = s * w2 * q2 * di * bendStiffness;
            var dp3 = s * w3 * q3 * di * bendStiffness;
            var dp4 = s * w4 * q4 * di * bendStiffness;
            verticesCorrectResult[cons.vIndex0] += dp1;
            verticesCorrectResult[cons.vIndex1] += dp2;
            verticesCorrectResult[cons.vIndex2] += dp3;
            verticesCorrectResult[cons.vIndex3] += dp4;
        }
    }
}

最后就是更新速度跟位置了。

参考资料

1. Position Based Dynamics

2.GAMES104-现代游戏引擎：从入门到实践 ---- 第十课 游戏引擎中物理系统的基础理论和算法

3.GPU布料物理模拟入门(牛顿力学) Github源码

4. CS114 Project 3:Cloth Simulation using Mass-Spring System

5. 最简化的PBD(基于位置的动力学)算法详解-论文原理讲解和太极代码

6. PBD 算法详解

7.物理模拟笔记-0-一个超简单PBD

8.PBD(Position Based Dynamics)学习笔记

9.基于Position Based Dynamics的布料模拟

10.Ten Minute Physics – 14 The secret of cloth simulation

9.SPlisHSPlasH is an open-source library for the physically-based simulation of fluids