物理模拟过程简介

发表于 2022-09-01 分类于物理，约束阅读次数：本文字数： 20k 阅读时长 ≈ 18 分钟

物理模拟流程

物理模拟循环主要有三个阶段构成：

碰撞检测（Collision Detection）
约束求解（Constraint Solving）
数值时间积分（Time Integration）

数值时间积分

欧拉公式

之前 PBD-Position Based Dynamics 中已经介绍过了，这里就不做过多介绍

韦尔莱（Verlet）积分

Verlet 积分法在 wiki 百科中的定义：

Verlet 积分法是经典力学（牛顿力学）中的一种最为普遍的积分方法，被广泛运用在分子运动模拟（Molecular Dynamics Simulation），行星运动以及织物变形模拟等领域。Verlet 算法要解决的问题是，给定粒子 $t$ 时刻的位置 $x$ 和速度 $v$，得到 $t+\Delta t$ 时刻的位置 $x(t+\Delta t)$ 和速度 $v(t+\Delta t)$。最简单的方法是前向计算（考虑当前和未来）的速度位移公式，也就是欧拉积分法，但精度不够，且不稳定。Verlet 积分是一种综合过去、现在和未来的计算方法（居中计算），精度为 $O(4)$, 稳定度好，且计算复杂度不比欧拉积分高多少。

总结一下：

verlet 积分与欧拉积分最大的差别就是：欧拉积分考虑当前和下一时刻，verlet 积分考虑上一时刻，当前，下一时刻
verlet 积分有着更好的精度，即4阶精度
verlet 积分和欧拉积分性能差不多

Verlet 主要思路

将 $x(t+\Delta t)$ 和 $x(t-\Delta t)$ 进行泰勒展开：

$$\begin{aligned}
\boldsymbol{x} (t+\Delta t) &= \boldsymbol{x}(t) + \frac{1}{1!} \frac{dx}{dt}\Delta t + \frac{1}{2!} \frac{d^2x}{dt2}\Delta t^2 + \frac{1}{3!} \frac{d^3x}{dt3}\Delta t^3 + O(\Delta t^4) \
&= \boldsymbol{x}(t) + \textcolor{SkyBlue}{\boldsymbol{v}{(t)}}\Delta t + \frac{1}{2!} \textcolor{SkyBlue}{\boldsymbol{a}} \Delta t^2 + \frac{1}{3!} \frac{d^3x}{dt3}\Delta t^3 + O(\Delta t^4) \
\boldsymbol{x} (t-\Delta t) &= \boldsymbol{x}(t) - \textcolor{SkyBlue}{\boldsymbol{v}{(t)}}\Delta t + \frac{1}{2!} \textcolor{SkyBlue}{\boldsymbol{a}} \Delta t^2 - \frac{1}{3!} \frac{d^3x}{dt3}\Delta t^3 + O(\Delta t^4)
\end{aligned}$$

两式相加可得 位置韦尔莱公式：

$$
\boldsymbol{x} (t + \Delta t) = 2\boldsymbol{x}(t) - \boldsymbol{x} (t-\Delta t) + \textcolor{SkyBlue}{\boldsymbol{a}} \Delta t^2 + O(\Delta t^4)
$$

两式相减，两边除以 $2\Delta t$，可得 速度韦尔莱公式：

$$
\boldsymbol{v} (t) = \frac{\boldsymbol{x}(t + \Delta t) - \boldsymbol{x} (t-\Delta t)}{2\Delta t} + O(\Delta t^2)
$$

这个式子显明，只有在知道前一时刻和后一时刻的位置时，才有可能知道当前时刻的速度。也就是说，在当前时刻不能获得速度信息，必须要等到下一时刻的位置确定以后，才能返回来计算当前的速度，因此速度的更新要晚一个时刻。

当然，开始模拟时我们需要知道 $\boldsymbol{x}(t-\Delta t)$，这个可以根据之前的泰勒展开得到（虽然这个获取方式精度只有 3 阶，但是长时间运行后，与总体误差相比还是可以忽略不计的）：

$$
\boldsymbol{x} (t-\Delta t) = \boldsymbol{x}(t) - \textcolor{SkyBlue}{\boldsymbol{v}{(t)}}\Delta t + \frac{1}{2!} \textcolor{SkyBlue}{\boldsymbol{a}} \Delta t^2 + O(\Delta t^3)
$$

碰撞检查

实际游戏运行过程中，物理模拟可能有很多个物体，如果采用简单粗暴的方法做碰撞检测，复杂度将会是 $O(n^2)$，因此为了优化效率，一般会将碰撞检测分成两个阶段：

粗略阶段（Broad Phase）：通过 AABB 检测两个物体是否碰撞
精确阶段（Narrow Phase）：粗略阶段计算碰撞后，精细阶段计算是否碰撞，碰撞点、碰撞方向以及碰撞深度

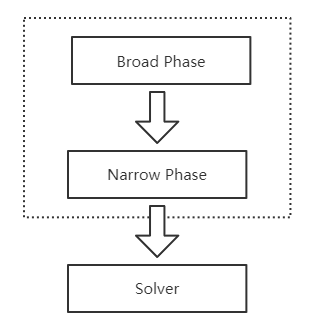
最后计算得到碰撞结果，进入求解器（Solver）来处理碰撞。

包围体

包围体：用简单的几何体来标识复杂外形的对象，如下图所示：

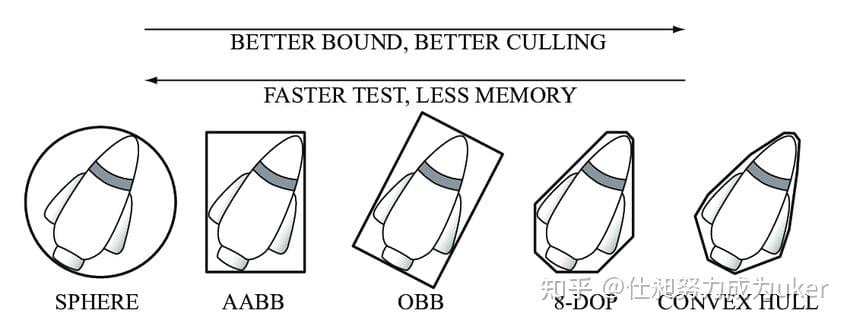
Sphere。用球体代表物体，只需要质心和半径就可以表示物体。求交操作简单，准确性较差。
AABB（axis-aligned bounding box）。AABB 的特点是包围体的各个面和边都垂直于世界坐标，这个特点带来的好处是求交操作简单。AABB 只需要两个对角点就可以表示物体。准确性一般。缺点是当实际物体发生旋转时，需要对 AABB 进行更新操作。
OBB（oriented bounding box）。与 AABB 相比，OBB 用最小包围盒代表物体，并且考虑物体的旋转。准确性比 AABB 好，但是求交操作更复杂。

除此之外，游戏中还会用到 胶囊体（Capsule） 来简化人物角色物理模拟。

粗略阶段（Broad Phase）

层次包围技术（BVH Bounding Volume Hierarchical）

简单来说，BVH 就是将 BV 用树的方式组织在一起，每个父节点是所有子节点 BV 的合并，并尽量保持每个节点的BV最小，BVH 可以非常方便地进行碰撞求交、射线求交。如下图：

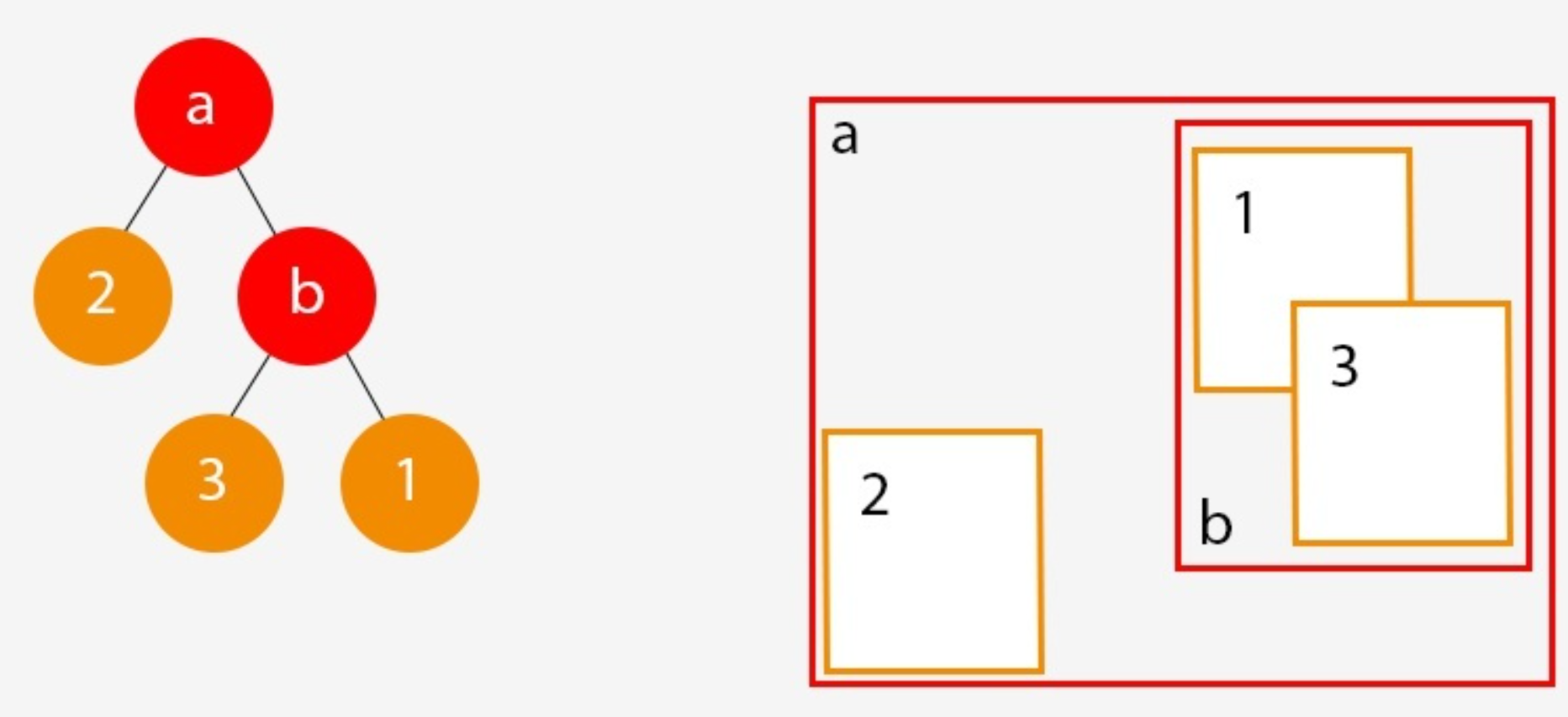
a ：根节点
b ：内部节点
1 2 3 ：叶子节点

碰撞检测过程：

碰撞求交

例如检查 3 跟有没有重叠的，先从根节点 a 开始，根节点总是跟子节点重叠，然后用根节点的子节点检查，最后发现 b 重叠，继续最终找到 1 跟 3 重叠。

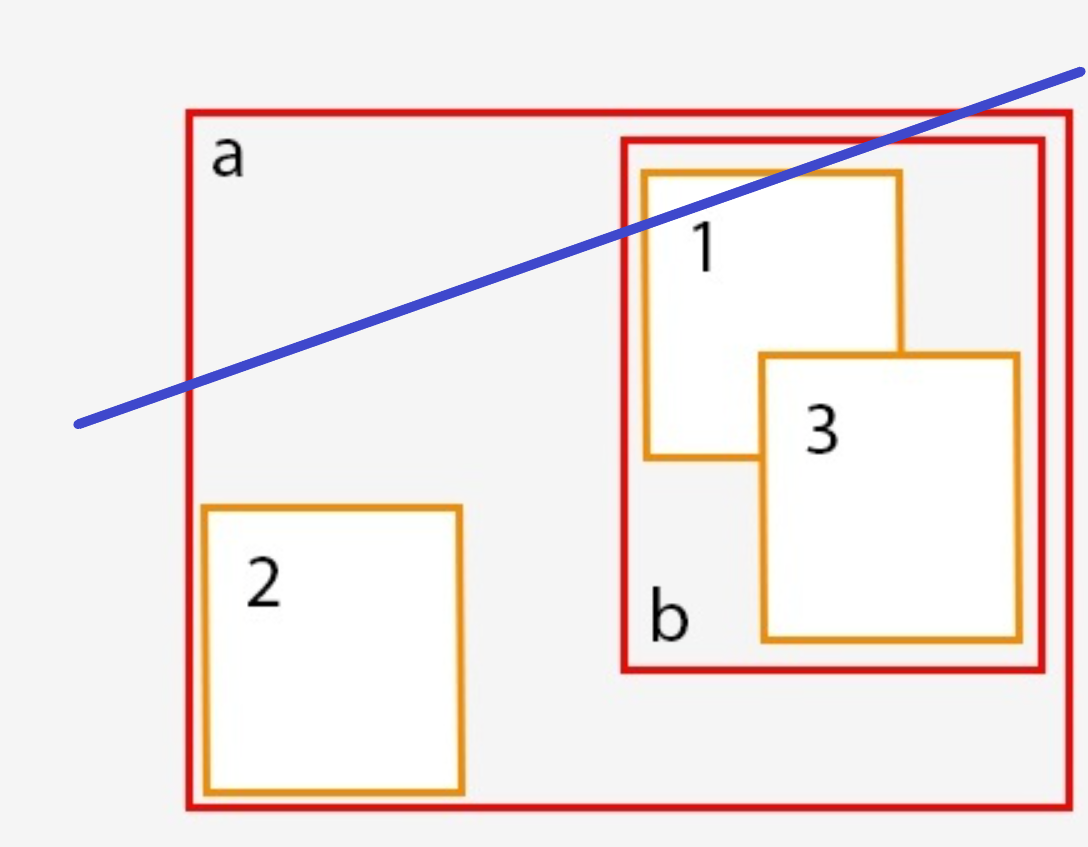
射线求交

同样射线求交过程一样，蓝色是检测射线，也是同样的过程

扫描剪除法（Sweep And Prune）

把所有物体的 AABB 投影到对应的坐标轴上，可以得到对应的 AABB 在对应轴的 AABB 的范围 [min, max]，一般情况下如果两个物体不重叠，范围不会重叠，一般来说二维判断需要分别映射到 x，y 轴。

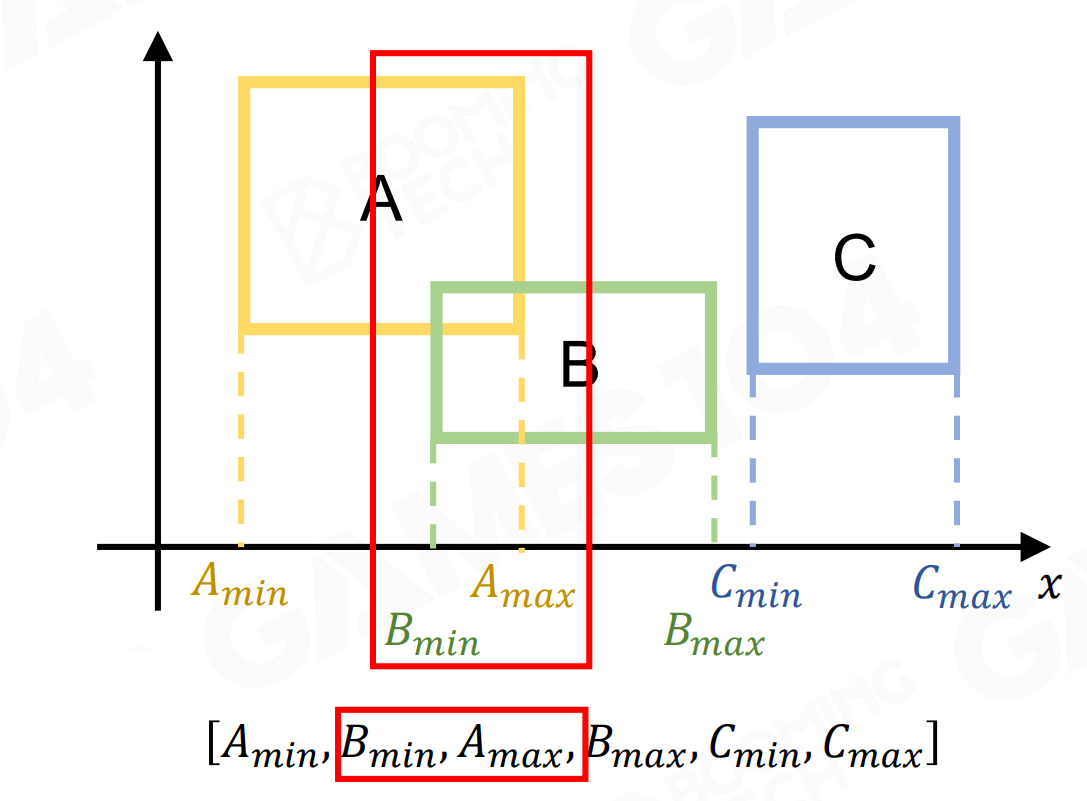
一般来说，对于已经排序好的数组来说，某个物体发生运动，对该物体的范围进行更新，时间效率其实很高。

精确阶段（Narrow Phase）

精确阶段需要计算出：

两个物体是否碰撞（碰撞体 $A$、$B$）
碰撞点
碰撞深度（最深穿透点 $P_A$、$P_B$)
碰撞法向量（$\vec{n}$）

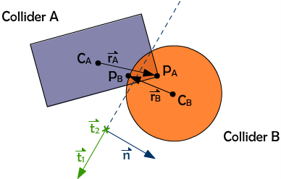
分离轴算法（SAT Separating Axis Test）

原理：两个凸多边形不相交，当且仅当必然存在一条直线，两个凸多边形在这条直线上的投影不相交。或者描述为:两个凸多边形相交，则在所有直线上的投影都是相交的。对于凸多面体也是一样的，只是投影在面上。

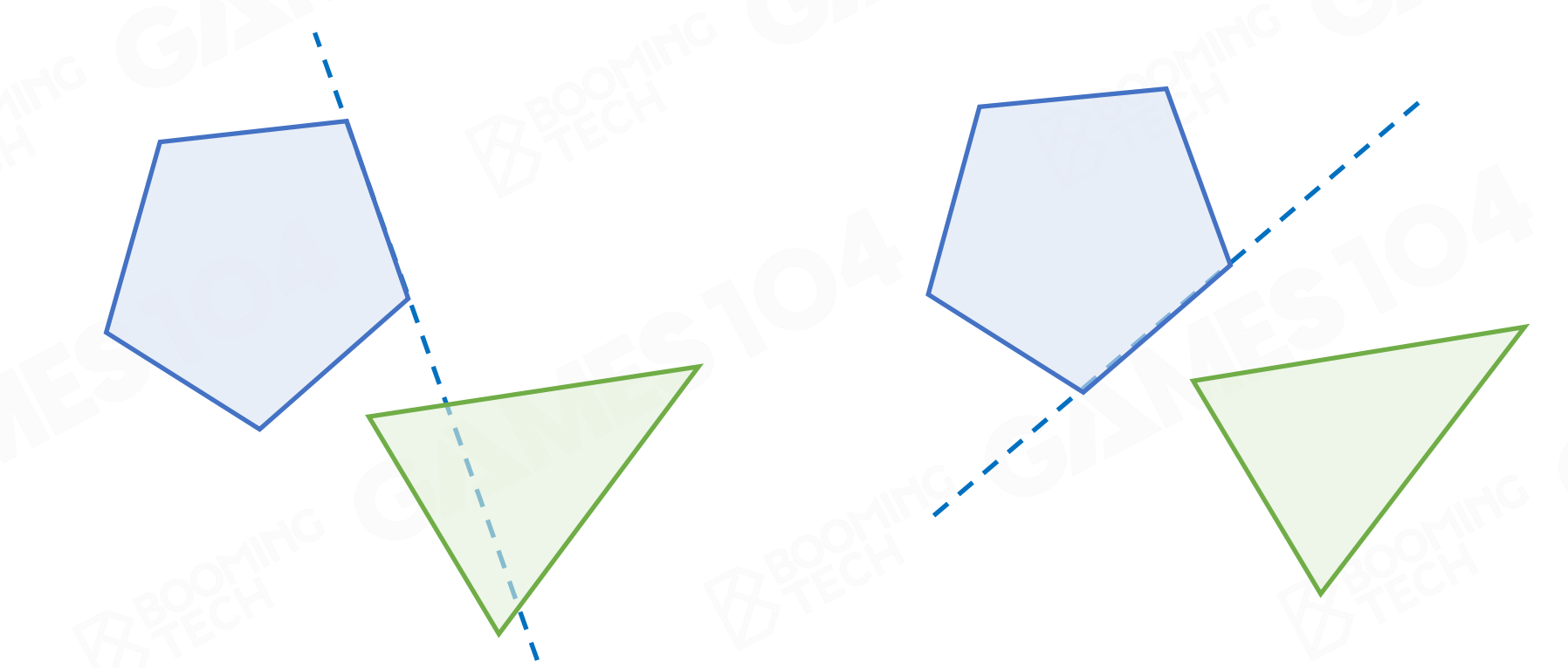
Gilbert-Johnson-Keerthi (GJK)算法

如果两个多边形相交，那么这两个多边形构成的闵可夫斯基差集(Minkowski Difference)，必然会包含原点。

闵可夫斯基和集(Minkowski Sum)

定义：两个图形 A, B 的闵可夫斯基和

$$
A \oplus B = { \vec{a} + \vec{b}; \vec{a} \in A, \vec{b} \in B}
$$

两个图形的闵可夫斯基和就是将其中一个图形中所有点到原点的向量，加上另外一个图形中所有的点到原点向量组成新点集图形

一个三角形跟一个点的闵可夫斯基和集：

如上图：三角形 $B$ 中的一个点向量加上点 $A$ 向量后得到新图形中的一个点

一个三角形跟另外一条线段的闵可夫斯基和集：

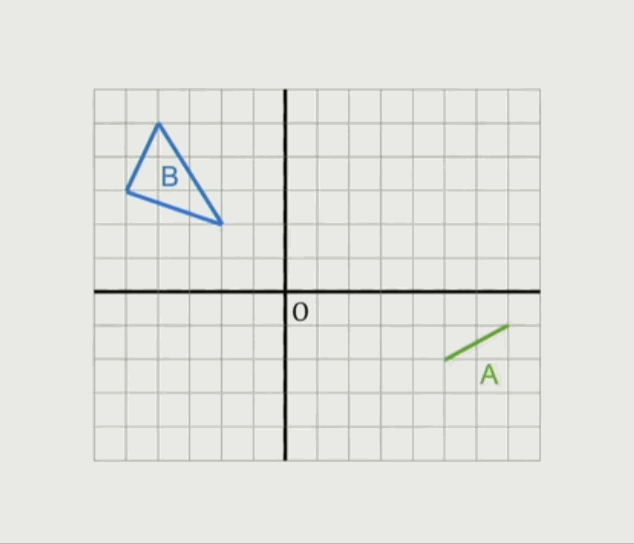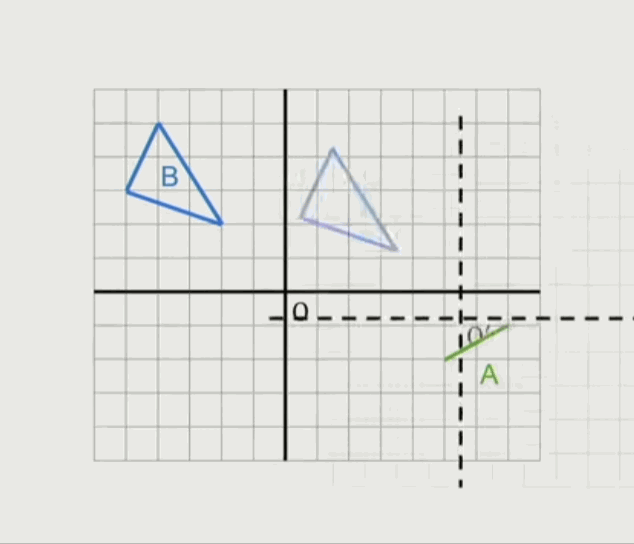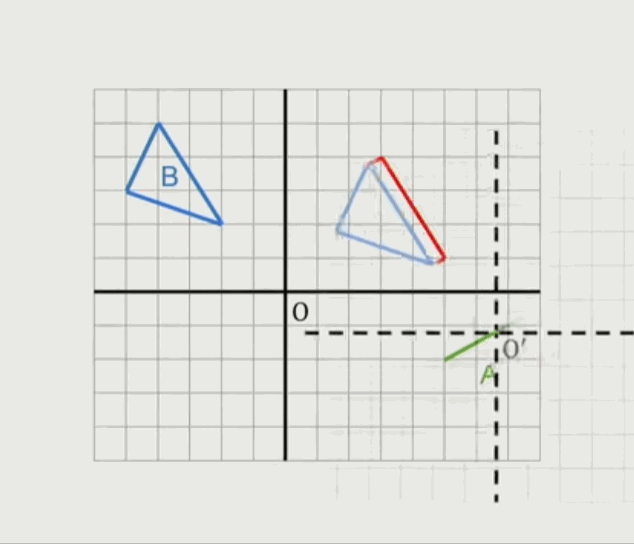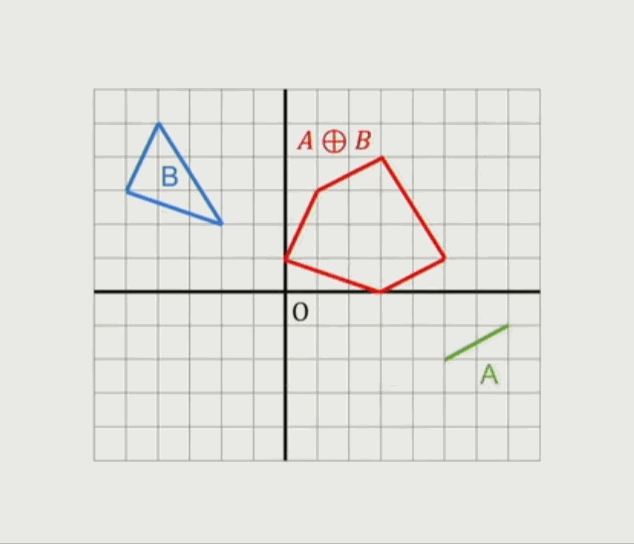
一个三角形跟另外一个三角形的闵可夫斯基和集：

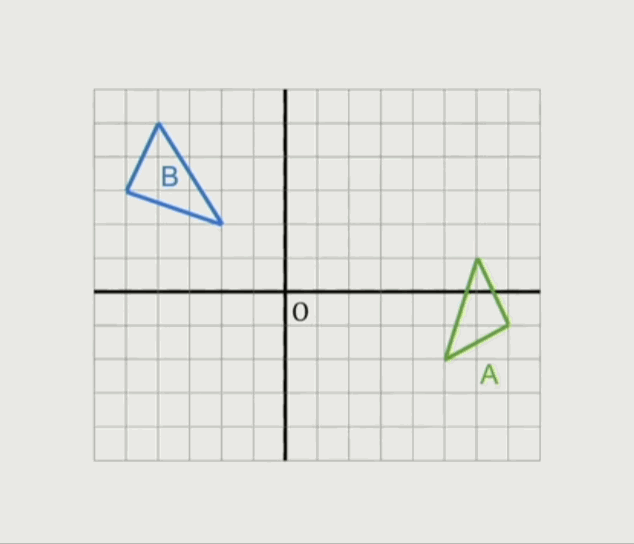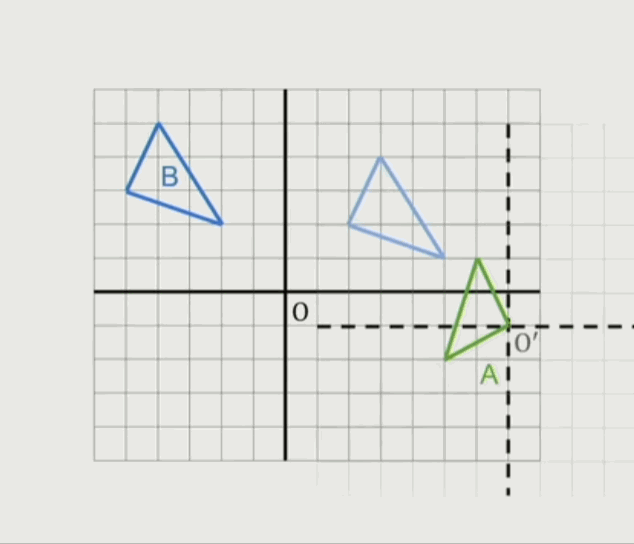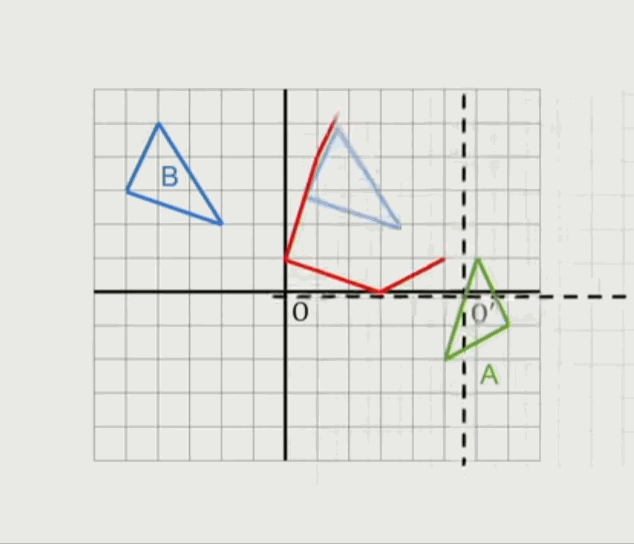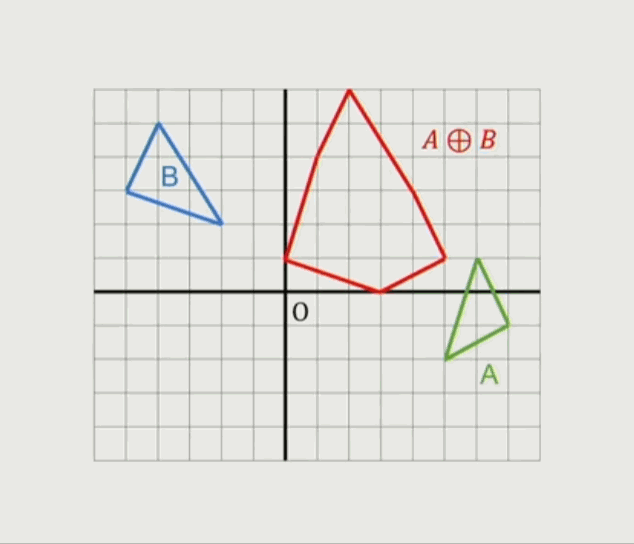
可以看出闵可夫斯基和集计算方式就是遍历一个多边形变的点到原点的向量，分别加上另外一个多边形边点到原点的向量所围成的新的多边形：

图中 $B$ 图形的各个点到原点向量分别加上图形 $A$ 中的点到原点的向量后，分别得到的粉色、蓝色、绿色点，围城的形状还是 $A$ 的样子。而且如果两个多面体都是图多边形，然最后形成的也是凸多边形。

闵可夫斯基差集(Minkowski Difference)

闵可夫斯基差集定义：

$$
A \ominus B = { \vec{a} - \vec{b}; \vec{a} \in A, \vec{b} \in B}
$$

如下图点集 $B$ 沿着原点做镜像，可以得到点集 $-B$（黄色三角形）

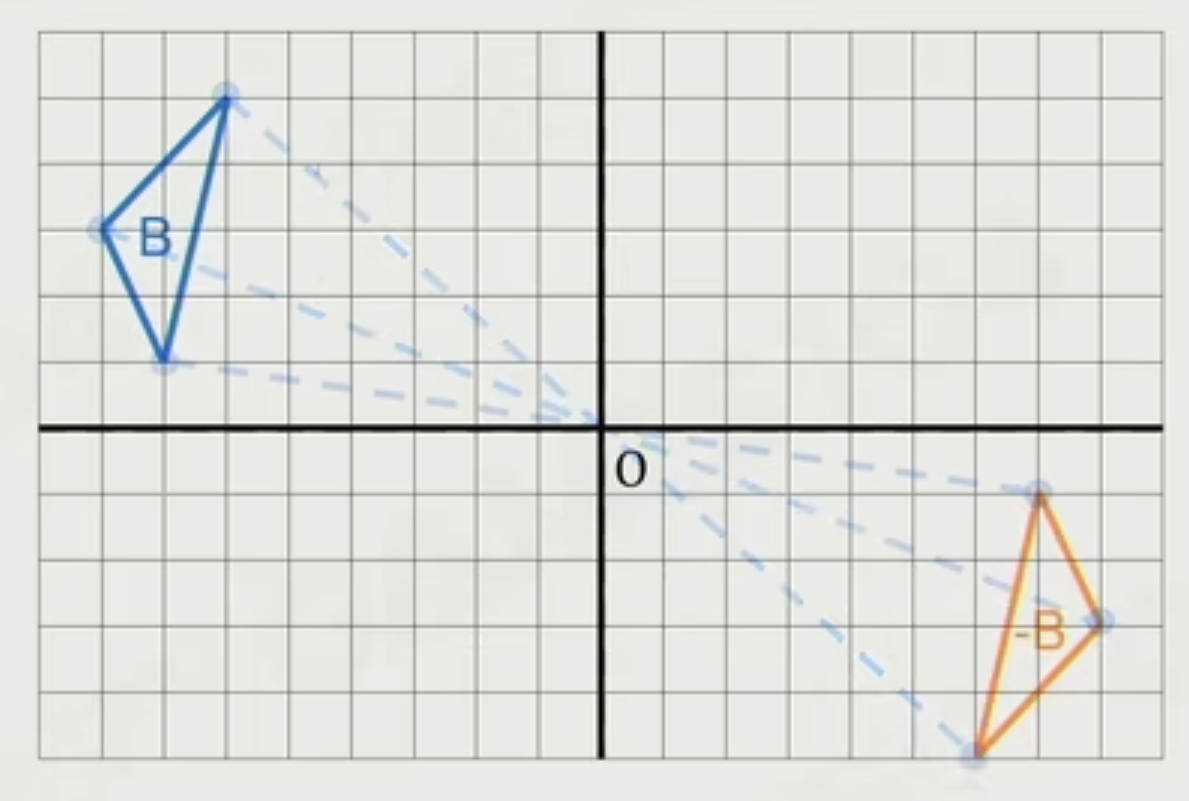
然后差集公式可以写成：

$$
A \ominus B = A \oplus (-B)
$$

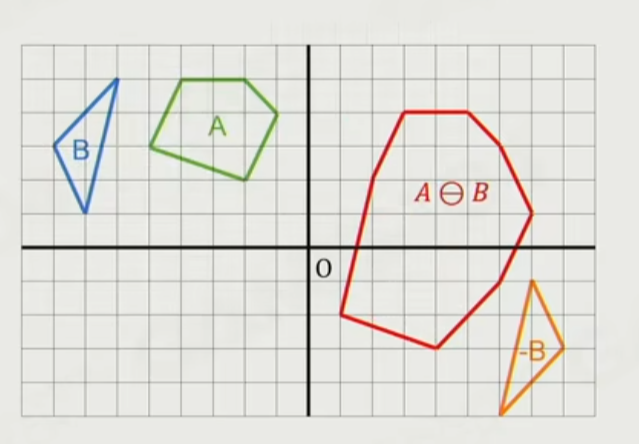
结论：如果两个点集的闵可夫斯基差集过原点，则表示这两个点集重叠：

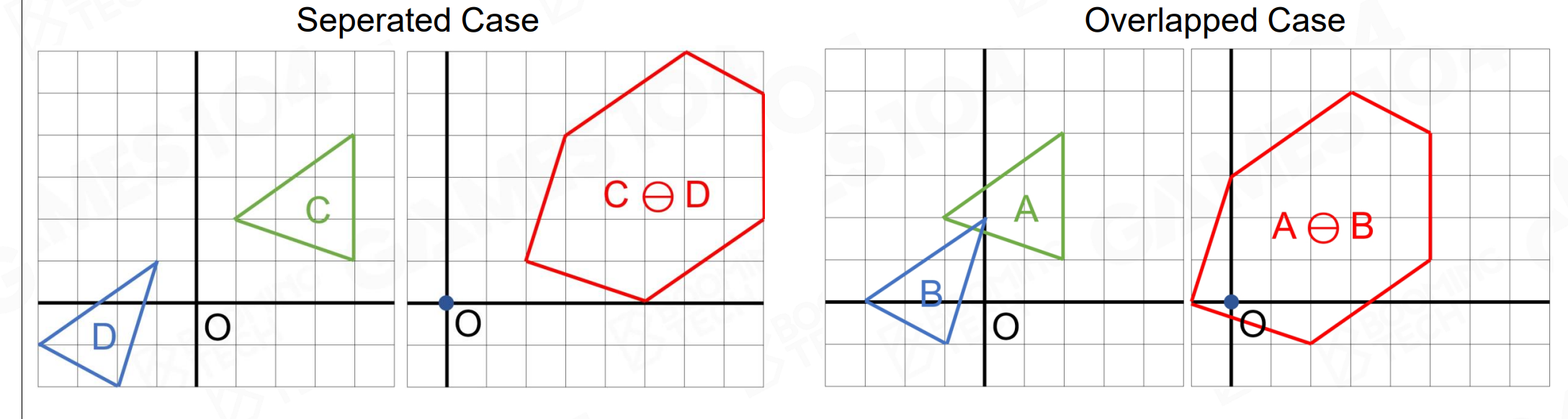
如果 $A$ $B$ 中有两个点重叠，那么这两个点向量做减法肯定得出零向量，即过原点。两个向量如果不为零向量，相加相减都不会得出零向量。

约束

等式约束

等式约束的定义如下:

$$
C=0
$$

如果我们要将某个物体坐标顶在某个原点则约束可以写为：

$$
\left[
\begin{matrix}
x \
y
\end{matrix}
\right] = 0
$$

不等式约束

$$
C > 0
$$

则当不满足条件 $C \leq 0$ 的时，我们要是的约束 $C = 0$，例如两个物体不能互相穿透，则他们之间的距离要大于 0，当他们距离小于 0 时，我们需要施加约束使得他们间的距离等于 0。

位置约束跟速度约束

当约束函数 $C=0$ 中的 $C$ 是一个位置的函数时，我们称之为位置约束，对应的速度约束就是对位置进行微分，得到速度约束。

$$\begin{aligned}
C &= 0 \qquad \dot{C} = 0 \
\left[
\begin{matrix}
x \
y
\end{matrix}
\right] &= 0 \qquad
\left[
\begin{matrix}
V_x \
V_y
\end{matrix}
\right] = 0
\end{aligned}$$

位置约束：会让物体立即满足约束
速度约束：物体会在约束条件下，慢慢满足约束，达到软性约束效果

实例：地面约束

我们要让物体不会掉到地面以下，只需要满足如下条件：

$$\begin{aligned}
y > 0 \qquad 若 \quad y \leq 0 \qquad 则 \qquad y &= 0 \
V_y &= 0
\end{aligned}$$

当一个物体陷入地面时，约束函数 $C$ 得出的结果不满足约束，计算出的结果其实就是

$$
C=误差量= y
$$

我们可以用这个误差量来修正速度 $V_y$（当 $V_y$不满足约束的时候，增加修正量），于是得出如下：

$$
V_y = 0 \rightarrow V_y + \frac{\beta}{\Delta t}y=0 \rightarrow V_y=-\frac{\beta}{\Delta t}y
$$

Baumgarte stabilization 邦加特修正
$\beta \in [0, 1]$ ：$\beta = 1$ 时，下一次积分计算速度位置时，就会完全修正误差，介于 $(0,1)$ 则会慢慢修正位置误差，$\beta = 0$ 表示不修正
$y$ 误差项（$y = 0$表示没有误差，此时满足约束）
$\Delta t$ 时间

代码实现 ⁴：

float dt = Time.deltaTime;
float y = Ball.transform.position.y;

vy += Gravity * dt;

if(y <= 0.0f)
{
    vy = -(Beta / dt) * y;
}

y += vy * dt;

Vector3 pos = Ball.transform.position;
pos.y = y;
Ball.transform.position = pos;

效果如下，当球掉落到地下后，会慢慢恢复上来：

一般形式

速度约束的一般形式可以写成（引入雅可比矩阵：Jacobian）：

$$
[J_{v_1} \quad J_{V_2}]\left[
\begin{matrix}
V_x \
V_y
\end{matrix}
\right] + b= 0
$$

$$
JV + b =0
$$

只考虑线性速度情况，一般来说二维约束包含三个自由度：两个线速度 $V_x$、$V_y$ 以及一个角速度 $\omega$，三维的约束包含六个自由度：线性速度 $V_x$、$V_y$、$V_z$ 角速度 $\omega_{x}$、$\omega_{y}$、$\omega_{z}$

地面约束一般形式

将之前的雅克比矩阵一般形式带入地面约束。

$$\begin{aligned}
JV + b = 0 &\qquad V_y + \frac{\beta}{\Delta t}y = 0 \
J = [0 \quad 1] &\qquad b = \frac{\beta}{\Delta t}y
\end{aligned}$$

J : 雅克比矩阵
b ：修正项

速度约束解析

当前速度 $V_1$ 约束不满足的时候，我们需要计算修正速度 $V_2$，于是有如下公式：

$$\begin{aligned}
MV &= \boldsymbol{L}\lambda \
M(V_2 - V_1) &= \boldsymbol{L}\lambda
\end{aligned}$$

$\boldsymbol{L}$：冲量方向
$\lambda$：冲量大小
$M=\left[\begin{matrix}
m \quad 0 \
0 \quad m
\end{matrix}
\right]$：质量矩阵

现在要求出 $\boldsymbol{L}$ 跟 $\lambda$。这里 $\boldsymbol{L}=J^T$，后面解释来源。带入可以直接得出：

$$
V_2 = V_1 + M^{-1}JT\lambda
$$

因为 $V_2$ 是修正后的速度，会满足约束，因此有：

$$\begin{aligned}
JV_2 + b &= 0 \
J(V_1 + M^{-1}JT\lambda) + b &= 0 \leftarrow (代入 V_2)
\end{aligned}$$

整理得出公式：

$$\begin{aligned}
(JM^{-1}JT)\lambda = -(JV_1 + b) \
\lambda = \frac{-(JV_1 + b)}{(JM^{-1}JT)}
\end{aligned}$$

一般来说会把分母项整理成一个形式，叫有效质量：

$$
M_{eff} = (JM^{-1}JT)^{-1}
$$

最后 $\lambda$ 会变成（拉格朗日乘数，也是修正 $V$ 的冲量大小）：

$$
\lambda = M_{eff}[-(JV_1 + b)]
$$

现在解释下 $\boldsymbol{L}$，假设我们这里 $V$ 是一个三维向量，则：

$$\begin{aligned}
JV + b &= 0 （雅克比参数展开）\
ax + by + cz + d &= 0 \rightarrow 平面方程
\end{aligned}$$

关于 $\boldsymbol{L}=J^T$
当一个点不在平面上时，带入这个等式，结果不等于 0，即不符合约束，如果要让这个点满足约束，最快的方向就是平面的法线向量 $\boldsymbol{n}=(a, b, c)$，也就是分别对函数求不同维度（x，y，z）的一阶导，就是 J，因此修正的冲量方向跟法相量平行。
$M(V_2 - V_1) = \boldsymbol{L}\lambda$ 公式中 $M$ 是 $2 * 2$ 维，速度是 $2 * 1$ 维，因此最后得出的 $\boldsymbol{L}$ 是 $2 * 1$ 维，而 $J$ 是 $1 * 2$维，因此得出 $\boldsymbol{L}=J^T$

打个比方：当前的位置是黑点，$C_1$ 和 $C_2$ 是需要满足的两个平面约束，当前点不满足这两个约束，因此需要依次使用这两个约束对位置做修正：

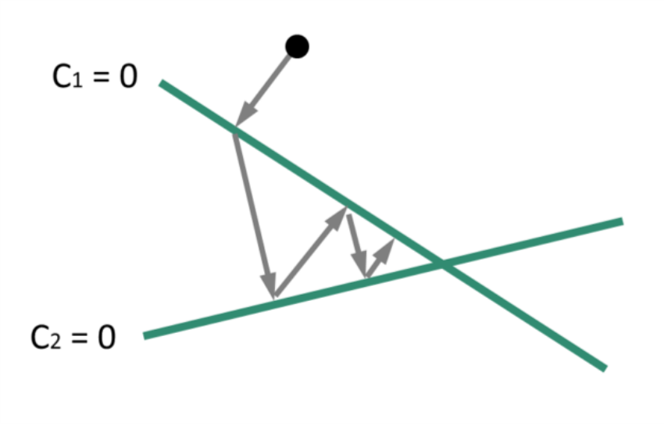
应用一般形式

将速度的一般形式应用到地面约束：

$$\begin{aligned}
JV + b & = 0 \
V_y + \frac{\beta}{\Delta t}y &= 0 \
[0 \quad 1]\left [\begin{matrix}
V_x \
V_y
\end{matrix}
\right] + \frac{\beta}{\Delta t}y &= 0
\end{aligned}$$

推算可得：

$$\begin{aligned}
J &= [0 \quad 1] \
b &= \frac{\beta}{\Delta t}y \
\lambda &= \frac{-(JV_1 + b)}{(JM^{-1}JT)} = M(-V_{y1} - \frac{\beta}{\Delta t}y) \
\Delta V &= M^{-1}JT\lambda=-V_{y1}-\frac{\beta}{\Delta t}y
\end{aligned}$$

$V_{y1}$：是 $V_y$ 一开始的速度

多重约束

之前有提到如果有两个约束，需要用迭代的方式交替修正位置，从而解出满足两个约束的共同解，如果不用迭代的方式，那就需要用到多重约束，先看二维的情况：

$$\begin{split}
J_1V + b_1 = 0 \
J_2V + b_2 = 0 \
\quad \
JV + b = 0 \
\quad \
J = \left[\begin{matrix}
J_1 \
J_2
\end{matrix}\right] \quad b = \left[\begin{matrix}
b1 \
b2
\end{matrix}\right]
\end{split}$$

$J$ 现在是一个 $2 * 2$ 矩阵

因此之前求解得到的 $\lambda$ 分母不再是标量，需要改写成：

$$\begin{aligned}
\lambda &= \frac{-(JV_1 + b)}{(JM^{-1}JT)} \downarrow \
\lambda &= (JM^{-1}JT)^{-1}[-(JV + b)] \
V_2 &= V_1 + M^{-1}JT\lambda
\end{aligned}$$

点约束

如果我们要将某个物体固定在某个点，则位置约束跟速度约束如下：

$$
C: \left[\begin{matrix}
x-P_x \
y - P_y
\end{matrix}\right] = 0 \
\quad \
\dot{C}: \left[\begin{matrix}
V_x \
V_y
\end{matrix}\right] = 0
$$

依次得出：

$$
JV + b = 0 \
J = \left[\begin{matrix}
1 \quad 0 \
0 \quad 1
\end{matrix}\right] \
\quad \
b = \frac{\beta}{\Delta t}C=\frac{\beta}{\Delta t}\left[\begin{matrix}
x - P_x \
y - P_y
\end{matrix}\right]
$$

$C$：之前提到过，一开始如果不满足约束，则约束得出的结果就是需要修正的量

根据上面得出的结论，最终算出：

$$\begin{aligned}
\lambda &= (JM^{-1}JT)^{-1}[-(JV + b)] \
\qquad \
V_2 &= V_1 + M^{-1}JT\lambda \
\Delta V &= M^{-1}JT\lambda = \frac{-\beta}{\Delta t}\left[\begin{matrix}
x - P_x \
y - P_y
\end{matrix}\right]
\end{aligned}
$$

当 $\beta = 1$ 时，下一次积分会立即修正，而当 $\beta \in (0, 1)$，则会慢慢修正

代码实现：

// P 是移动物体
// Ball 是跟随物体，会跟随 P 移动，即位置固定成 P 的位置

float dt = Time.deltaTime;
Vector3 c = Ball.transform.position - P.transform.position;

v += (-Beta / dt) * c;
// 阻尼消耗
v *= 0.9f;
Ball.transform.position += v*dt;

代码效果如下：

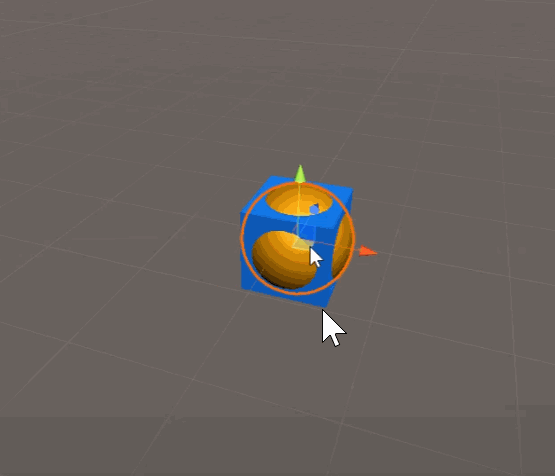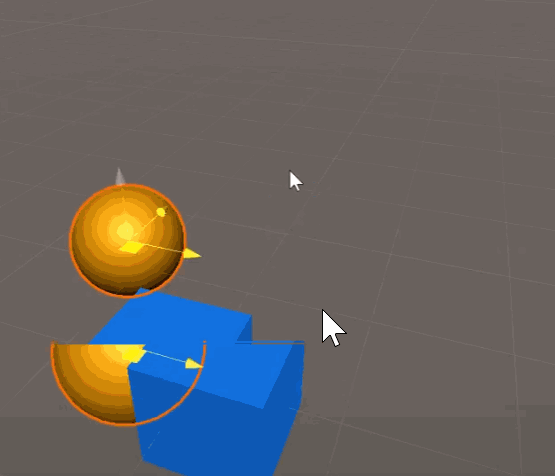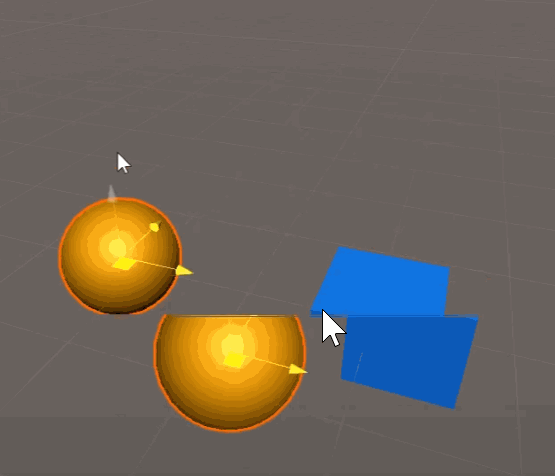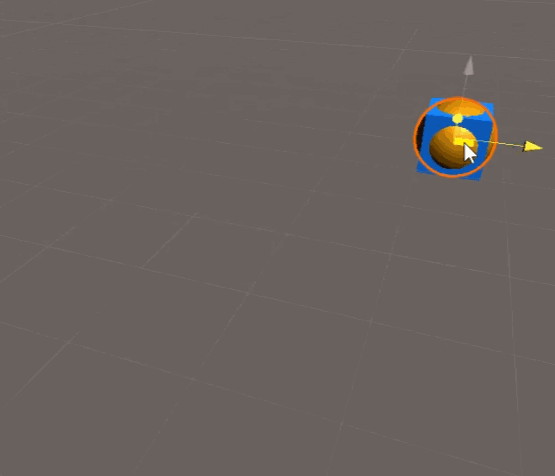
旋转跟转动惯量

之前考虑的都是二维的情况，现在加入旋转，自由度由两个变成三个:

$$
\left[\begin{matrix}
x \
y
\end{matrix}
\right] \rightarrow \left[\begin{matrix}
x \
y \
a \
\end{matrix}\right] \
\qquad \
V = \left[\begin{matrix}
V_x \
V_y
\end{matrix}
\right] \rightarrow \left[\begin{matrix}
V_x \
V_y \
\omega \
\end{matrix}\right] \
\qquad \
M = \left[\begin{matrix}
m \quad 0 \
0 \quad m
\end{matrix}
\right] \rightarrow \left[\begin{matrix}
m \quad 0 \quad 0 \
0 \quad m \quad 0 \
0 \quad 0 \quad \boldsymbol{I} \
\end{matrix}\right] \
$$

最终的求解形式不变

$$\begin{aligned}
JV &+ b = 0 \
\lambda &= (JM^{-1}JT)^{-1}[-(JV + b)]
\end{aligned}
$$

$\boldsymbol{I}$ 是二维的转动惯量

旋转约束

现在看下旋转约束：

$$
C: a - \theta = 0 \
\dot{C}: \omega = 0
$$

套用一般形式：

$$\begin{aligned}
JV &+ b = 0 \
J &= [0 \quad 0 \quad 1] \
b &= \frac{\beta}{\Delta t}C = \frac{\beta}{\Delta t}\left[\begin{matrix}
0 \
0 \
a - \theta
\end{matrix}\right]
\end{aligned}$$

最后算出结果（$\lambda$ 跟 $V_2$ 的形式都没变化，只是最后的结果 $\Delta V$ 不一样）：

$$\begin{aligned}
\lambda &= (JM^{-1}JT)^{-1}[-(JV + b)] \
\qquad \
V_2 &= V_1 + M^{-1}JT\lambda \
\Delta V &= M^{-1}JT\lambda = \frac{-\beta}{\Delta t}\left[\begin{matrix}
0 \
0 \
a - \theta
\end{matrix}\right]
\end{aligned}
$$

晋升到 3D 约束

$$\begin{split}
JV + b = 0 \quad V = \left[\begin{matrix}
V_x \
V_y \
V_z \
\omega_x \
\omega_y \
\omega_z
\end{matrix}\right] \quad M = \begin{bmatrix}\begin{matrix}
m&0&0\
0&m&0\
0&0&m
\end{matrix} & \begin{matrix}
0&0&0\
0&0&0\
0&0&0
\end{matrix} \ \begin{matrix}
0&0&0\
0&0&0\
0&0&0
\end{matrix} & \boxed{\boldsymbol{I}}
\end{bmatrix} \quad \
M^{-1} = \begin{bmatrix}\begin{matrix}
\frac{1}{m}&0&0\
0&\frac{1}{m}&0\
0&0&\frac{1}{m}
\end{matrix} & \begin{matrix}
0&0&0\
0&0&0\
0&0&0
\end{matrix} \ \begin{matrix}
0&0&0\
0&0&0\
0&0&0
\end{matrix} & \boxed{\boldsymbol{I^{-1}}}
\end{bmatrix}
\end{split}
$$

$V_x$、$V_y$、$V_z$ 是线性速度的分量，$\omega$ 是一个三维向量 $\omega_x$、$\omega_y$、$\omega_z$ 是它的分量，方向是角速度的旋转轴向，长度是角速度的大小 \
形状不同的物体转动惯量 $I$ 不一样，具体参考⁵

点约束 + 旋转

最后一个例子：正方体一个角钉在空间中的某个点（$P$ 点线速度为 $0$，质心 $X$ 到 $P$ 点距离固定）

假设将右手（除了大拇指以外）的手指顺着转动的方向朝内弯曲，则大拇指所指的方向即是角速度向量的方向。

$$
C:(X + \boldsymbol{R}) - P = 0 \
\qquad \
\dot{C} = \left[\begin{matrix}
V_x \
V_y \
V_z
\end{matrix}\right] + \left[\begin{matrix}
\omega_x \
\omega_y \
\omega_z
\end{matrix}\right] \times \left[\begin{matrix}
R_x \
R_y \
R_z
\end{matrix}\right] = \left[\begin{matrix}
0 \
0 \
0
\end{matrix}\right]
$$

$X$：立方体位置
$\boldsymbol{R}$：中心到角落的向量
$P$：空间定住的点
做微分后，$P$ 常数项，微分后为 $0$
刚体速度公 $\dot{C}$ 式查阅 ⁷

带入一般方程（将 $\dot{C}$ 写成雅克比矩阵形式）：

$$\begin{aligned}
JV &+ b = 0 \
J &= \left[\begin{array}{ccc:ccc}
1 & 0 & 0 & 0 & R_z & -R_y \
0 & 1 & 0 & -R_z & 0 & R_x \
0 & 0 & 1 &R_y & -R_x & 0
\end{array}\right] \
\qquad \
&= [E \quad S] \
\qquad \
E &= \left[\begin{matrix}
1 & 0 & 0 \
0 & 1 & 0 \
0 & 0 & 1
\end{matrix}\right] \
\qquad \
S &= \left[\begin{matrix}
0 & R_z & -R_y \
-R_z & 0 & R_x \
R_y & -R_x & 0
\end{matrix}\right]
\end{aligned}
$$

$S$ 是两个向量的叉积矩阵
对照 $\dot{C}$ 的形式，既可以知道 $J$ 是一个 $3 * 6$ 的矩阵，速度 $V$ 是一个 $6 * 1$ 的矩阵，$JV$

开始推导过程：

$$\begin{aligned}
b &= \frac{\beta}{\Delta t} C \
C &= (X + \boldsymbol{R}) - P \
M &= \left[\begin{matrix}
mE & 0\
0 & 1
\end{matrix}\right] \
\qquad \
\lambda &= (JM^{-1}JT)^{-1}[-(JV + b)] \
&= \left([E \quad S] \left[\begin{matrix}
\frac{1}{m}E & 0 \
0 & \boldsymbol{I}^{-1}
\end{matrix}\right] \left[\begin{matrix}
E \
S^T
\end{matrix}\right]\right)^{-1} [-(JV+b)] \
&= (\frac{1}{m}E+S\boldsymbol{I}^{-1}ST)^{-1}[-(JV+b)] \
\qquad \
\Delta V &= M^{-1}JT\lambda=\left[\begin{matrix}
\frac{1}{m}\lambda \
\quad \
\boldsymbol{I}^{-1}ST\lambda
\end{matrix}\right]
\end{aligned}$$

代码实现以及注释：

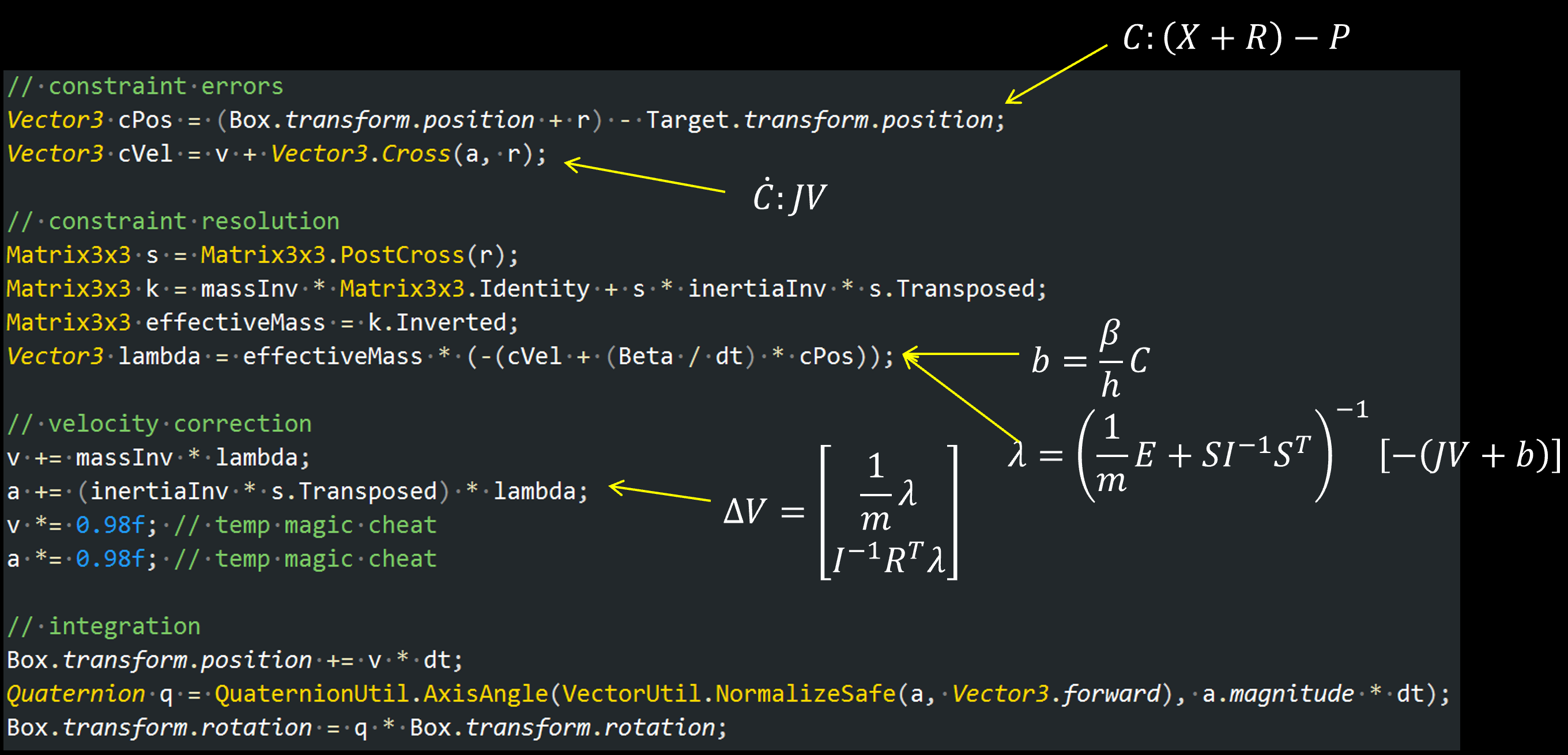
$a$：是角速度

运行效果：

总结

速度约束解析过程：

将速度约束方程写成对应的雅克比方程形式，得出雅克比矩阵 $J$ 跟速度矩阵 $V$
$$
JV + b = 0
$$
然后根据约束方程，求解满足约束的速度 $V_2$，最后得出速度变化量： $\Delta V = V_2 - V_1$，根据冲量公式，计算出冲量大小 $\lambda$
$$\begin{aligned}
MV &= FT \
\quad \
M( V_2 - V_1)&=\boldsymbol{L}\lambda \quad {\small \leftarrow \boldsymbol{L} = J^T} \
\quad \
\Delta V = V_2 - V_1 &= M^{-1}JT\lambda
\end{aligned}
$$
最后求解冲量大小： $\lambda$
$$
\lambda = (JM^{-1}JT)^{-1}[-(JV + b)] \quad {\small V:一开始的速度矩阵}
$$
最后将每次迭代得到的 $\Delta V$ 叠加到速度上，经过多次迭代，最终满足约束条件

碰撞接触约束

现在介绍如何来求解碰撞接触约束：

已知条件：

$A$ 是长形状碰撞体，质心为 $C_A$
$B$ 是球形碰撞体，质心为 $C_B$
碰撞深度点为 $P_A$、$P_B$
质心到碰撞点的向量分别为：$\boldsymbol{r_A}$、 $\boldsymbol{r_B}$
碰撞法向量：$\boldsymbol{n}$，法向量的两个垂直向量为：$\boldsymbol{t_1}$、 $\boldsymbol{t_2}$（$\boldsymbol{t_2}$ 垂直于这个平面朝外，因此图上看不到）

位置约束方程（$P_B$、$P_A$）：

$$\begin{aligned}
C:& (P_B - P_A) \cdot \boldsymbol{n} \geq 0 \
& (C_B + \boldsymbol{r_B} - C_A - \boldsymbol{r_A}) \geq 0
\end{aligned}$$

速度约束方程（$P_A$、$P_B$ 点之间的相对速度与$\boldsymbol{n}$内积大于等于 0）：

$$
\dot{C}:(-V_A - \omega_A \times \boldsymbol{r_A} + V_B + \omega_B \times \boldsymbol{r_B}) \cdot \boldsymbol{n} \geq 0
$$

代入之前的雅各比方程中：

$$\begin{aligned}
JV &+ b \geq 0 \qquad V = \left[\begin{matrix}
V_A \
\omega_A \
V_B \
\omega_B
\end{matrix}\right] \
\qquad \
J &= [-\boldsymbol{n}^T \quad (-\boldsymbol{r}_A \times \boldsymbol{n})^T \quad \boldsymbol{n}^T \quad (\boldsymbol{r}_B \times \boldsymbol{n}^T) ] \
\qquad \
\lambda &= (JM^{-1}JT)^{-1}[-(JV + b)] \quad M = \left[\begin{matrix}
M_A & 0 & 0 & 0 \
0 & I_A & 0 & 0 \
0 & 0 & M_B & 0 \
0 & 0 & 0 & I_B
\end{matrix}\right]
\end{aligned}
$$

最终得出

$$\begin{aligned}
M_{eff}^{-1} = (JM^{-1}JT) = & -\boldsymbol{n} \cdot M_A^{-1} \cdot (-\boldsymbol{n}) \
& + (-\boldsymbol{r}_A \times \boldsymbol{n}) \cdot I_A^{-1} (-\boldsymbol{r}_A \times \boldsymbol{n}) \
& + \boldsymbol{n} \cdot M_B^{-1} \cdot \boldsymbol{n} \
& + (-\boldsymbol{r}_B \times \boldsymbol{n}) \cdot I_B^{-1} (-\boldsymbol{r}_B \times \boldsymbol{n}) \
\quad \
= & \quad M_A^{-1} \
& + (-\boldsymbol{r}_A \times \boldsymbol{n}) \cdot I_A^{-1} (-\boldsymbol{r}_A \times \boldsymbol{n}) \
& + M_B^{-1} \
& + (-\boldsymbol{r}_B \times \boldsymbol{n}) \cdot I_B^{-1} (-\boldsymbol{r}_B \times \boldsymbol{n}) \
\end{aligned}
$$

Tips：

$M_A$、$M_B$ 是常数

总约束限制

碰撞约束解析的迭代过程中，会出现总冲量为负的情况，这样会导致物体越陷越深，因此限制这个总冲量必须为正。

$$
\sum{\lambda_i \geq 0}
$$

初始化代码如下：

// dir    : 法向量
// m_va   : J 矩阵中 A 线速度参数
// m_wa   : J 矩阵中 A 角速度参数
// m_vb   : J 矩阵中 B 线速度参数
// m_wb   : J 矩阵中 B 角速度参数

public void Init(Contact contact, Vector3 dir, float dt)
{
    // J 矩阵
    m_va = -dir;
    m_wa = -Vector3.Cross(contact.m_rA, dir);
    m_vb = dir;
    m_wb = Vector3.Cross(contact.m_rB, dir);

    // JV + b = 0
    // 参数 b : 下个点会讲到如何求解 b
    m_bias = 0.0f;

    // M_eff 的倒数
    float k = 
        contact.BodyA.InverseMass 
        + Vector3.Dot(m_wa, contact.BodyA.InverseInertiaWs * m_wa) 
        + contact.BodyB.InverseMass 
        + Vector3.Dot(m_wb, contact.BodyB.InverseInertiaWs * m_wb);

    m_effectiveMass = 1.0f / k;
    m_totalLambda = 0.0f;
}

迭代过程中，约束求解代码：

public void Resolve(Contact contact, float dt)
{
    Vector3 dir = m_vb;

    // JV = Jacobian * velocity vector
    float jv = 
        Vector3.Dot(m_va, contact.BodyA.LinearVelocity) 
        + Vector3.Dot(m_wa, contact.BodyA.AngularVelocity) 
        + Vector3.Dot(m_vb, contact.BodyB.LinearVelocity) 
        + Vector3.Dot(m_wb, contact.BodyB.AngularVelocity);

    // raw lambda
    float lambda = m_effectiveMass * (-(jv + m_bias));
    
    // lambda 不能小于 0
    m_totalLambda = Mathf.Max(0.0f, m_totalLambda + lambda);

    lambda = m_totalLambda - oldTotalLambda;

    // velocity correction
    contact.BodyA.LinearVelocity += contact.BodyA.InverseMass * m_va * lambda;
    contact.BodyA.AngularVelocity += contact.BodyA.InverseInertiaWs * m_wa * lambda;
    contact.BodyB.LinearVelocity += contact.BodyB.InverseMass * m_vb * lambda;
    contact.BodyB.AngularVelocity += contact.BodyB.InverseInertiaWs * m_wb * lambda;
}

偏重 b

前面解算的都是针对速度约束，解出 $\lambda$，现在带入位置约束参数 $b$

$$\begin{aligned}
J&V + \underline{b} = 0 \
\quad \
C&:(P_B-P_A) \cdot \boldsymbol{n} \
\quad \
b &= \frac{\beta}{\Delta t}C = \frac{\beta}{\Delta t}(P_B - P_A) \cdot \boldsymbol{n}
\end{aligned}
$$

上述的误差参数 $b$ 只能让两个物体分开，不在重叠，如果想要达到两个物体碰撞后分别按照碰撞反方向弹开的效果，需要加入新的约束量：

$$
b = \frac{\beta}{\Delta t}C = \frac{\beta}{\Delta t}(P_B - P_A) \cdot \boldsymbol{n} + \boxed {C_R(-V_A - \omega_A \times \boldsymbol{r_A} + V_B + \omega_B \times \boldsymbol{r_B}) \cdot \boldsymbol{n}}
$$

Tips：

$C_R$ : 弹性系数 $C_R=0$ 表示完全非弹性碰撞，两个物体碰撞后合为一体， $C_R=1$ 为完全弹性碰撞，两个物体碰撞后，按照之前速度，反方向弹开。

加上偏差量 $b$ 后的代码实现：

// dir    : 法向量
// m_va   : J 矩阵中 A 线速度参数
// m_wa   : J 矩阵中 A 角速度参数
// m_vb   : J 矩阵中 B 线速度参数
// m_wb   : J 矩阵中 B 角速度参数

public void Init(Contact contact, Vector3 dir, float dt)
{
    // J 矩阵
    m_va = -dir;
    m_wa = -Vector3.Cross(contact.m_rA, dir);
    m_vb = dir;
    m_wb = Vector3.Cross(contact.m_rB, dir);

    // JV + b = 0
    // 参数 b 
    m_bias = 0.0f;

    // beta: 邦加特参数 β
    float beta = contact.BodyA.ContactBeta * contact.BodyB.ContactBeta;

    // restitution : 弹性碰撞系数 C_R
    float restitution = contact.BodyA.Restitution * contact.BodyB.Restitution;

    // 两点的相对速度
    Vector3 relativeVelocity =
        -contact.BodyA.LinearVelocity
        - Vector3.Cross(contact.BodyA.AngularVelocity, contact.m_rA)
        + contact.BodyB.LinearVelocity
        + Vector3.Cross(contact.BodyB.AngularVelocity, contact.m_rB);
    float closingVelocity = Vector3.Dot(relativeVelocity, dir);

    // Penetration ： 碰撞深度在碰撞法线上的投影长度
    m_bias = -(beta / dt) * contact.Penetration + restitution * closingVelocity;

    // M_eff 的倒数
    float k = 
        contact.BodyA.InverseMass 
        + Vector3.Dot(m_wa, contact.BodyA.InverseInertiaWs * m_wa) 
        + contact.BodyB.InverseMass 
        + Vector3.Dot(m_wb, contact.BodyB.InverseInertiaWs * m_wb);

    m_effectiveMass = 1.0f / k;
    m_totalLambda = 0.0f;
}

摩擦力

两个物体碰撞时，如果物体自身带旋转、侧面碰撞，那么在碰撞点切面方向会发生摩擦，因此要在两个切线方向加上摩擦力，雅克比矩阵形式类似之前的速度约束公式，只是将方向变成切线方向 $\boldsymbol{t_1}$、$\boldsymbol{t_2}$。

$$\begin{aligned}
J_n &= [-\boldsymbol{n}^T \quad (-\boldsymbol{r}_A \times \boldsymbol{n})^T \quad \boldsymbol{n}^T \quad (\boldsymbol{r}B \times \boldsymbol{n}^T) ] \qquad \lambda_n \geq 0 \
\qquad \
J{t_1} &= [-\boldsymbol{t_1}^T \quad (-\boldsymbol{r}A \times \boldsymbol{t_1})^T \quad \boldsymbol{t_1}^T \quad (\boldsymbol{r}B \times \boldsymbol{t_1}^T) ] \qquad -\mu \lambda_n \leq \lambda{t_1} \leq \mu \lambda_n \
\qquad \
J{t_2} &= [-\boldsymbol{t_2}^T \quad (-\boldsymbol{r}_A \times \boldsymbol{t_2})^T \quad \boldsymbol{t_2}^T \quad (\boldsymbol{r}B \times \boldsymbol{t_2}^T) ] \qquad -\mu \lambda_n \leq \lambda{t_2} \leq \mu \lambda_n \
\end{aligned}
$$

Tips：

$\lambda$ : 是冲力大小
$\mu$ ：摩擦力系数
摩擦力方向跟冲力方向相反，因此范围是 $-\mu \lambda_n \leq \lambda_{t} \leq \mu \lambda_n$

将摩擦力约束加入后代码如下：

public void InitVelocityConstraint(float dt)
{
    m_rA = PositionA - BodyA.CenterOfMassWs;
    m_rB = PositionB - BodyB.CenterOfMassWs;

    Vector3 tangent;
    Vector3 bitangent;
    VectorUtil.FormOrthogonalBasis(Normal, out tangent, out bitangent);

    m_jN = new Jacobian(Jacobian.Type.Normal);
    m_jT = new Jacobian(Jacobian.Type.Tangent);
    m_jB = new Jacobian(Jacobian.Type.Tangent);

    // 速度约束
    m_jN.Init(this, Normal, dt);
    // 切线1 摩擦力
    m_jT.Init(this, tangent, dt);
    // 切线2 摩擦力
    m_jB.Init(this, bitangent, dt);
}

public void SolveVelocityConstraint(float dt)
{
    m_jN.Resolve(this, dt);
    m_jT.Resolve(this, dt);
    m_jB.Resolve(this, dt);
}

// 初始化跟之前一样，摩擦力 bias 为 0
public void Init(Contact contact, Vector3 dir, float dt)
{
    m_va = -dir;
    m_wa = -Vector3.Cross(contact.m_rA, dir);
    m_vb = dir;
    m_wb = Vector3.Cross(contact.m_rB, dir);

    m_bias = 0.0f;
    if (m_type == Type.Normal)
    {
        float beta = contact.BodyA.ContactBeta * contact.BodyB.ContactBeta;
        float restitution = contact.BodyA.Restitution * contact.BodyB.Restitution;
        Vector3 relativeVelocity =
        -contact.BodyA.LinearVelocity
        - Vector3.Cross(contact.BodyA.AngularVelocity, contact.m_rA)
        + contact.BodyB.LinearVelocity
        + Vector3.Cross(contact.BodyB.AngularVelocity, contact.m_rB);
        float closingVelocity = Vector3.Dot(relativeVelocity, dir);
        m_bias = -(beta / dt) * contact.Penetration + restitution * closingVelocity;
    }

    float k = 
        contact.BodyA.InverseMass 
        + Vector3.Dot(m_wa, contact.BodyA.InverseInertiaWs * m_wa) 
        + contact.BodyB.InverseMass 
        + Vector3.Dot(m_wb, contact.BodyB.InverseInertiaWs * m_wb);

    m_effectiveMass = 1.0f / k;
    m_totalLambda = 0.0f;
}

public void Resolve(Contact contact, float dt)
{
    Vector3 dir = m_vb;

    // JV = Jacobian * velocity vector
    float jv = 
        Vector3.Dot(m_va, contact.BodyA.LinearVelocity) 
        + Vector3.Dot(m_wa, contact.BodyA.AngularVelocity) 
        + Vector3.Dot(m_vb, contact.BodyB.LinearVelocity) 
        + Vector3.Dot(m_wb, contact.BodyB.AngularVelocity);

    // raw lambda
    float lambda = m_effectiveMass * (-(jv + m_bias));

    // clamped lambda
    //   normal  / contact resolution  :  lambda >= 0
    //   tangent / friction            :  -maxFriction <= lambda <= maxFriction
    float oldTotalLambda = m_totalLambda;
    switch (m_type)
    {
        case Type.Normal:
            m_totalLambda = Mathf.Max(0.0f, m_totalLambda + lambda);
        break;

        // 限制摩擦力
        case Type.Tangent:
            float friction = contact.BodyA.Friction * contact.BodyB.Friction;
            float maxFriction = friction * contact.m_jN.m_totalLambda;
            m_totalLambda = Mathf.Clamp(m_totalLambda + lambda, -maxFriction, maxFriction);
        break;
    }
    lambda = m_totalLambda - oldTotalLambda;

    // velocity correction
    contact.BodyA.LinearVelocity += contact.BodyA.InverseMass * m_va * lambda;
    contact.BodyA.AngularVelocity += contact.BodyA.InverseInertiaWs * m_wa * lambda;
    contact.BodyB.LinearVelocity += contact.BodyB.InverseMass * m_vb * lambda;
    contact.BodyB.AngularVelocity += contact.BodyB.InverseInertiaWs * m_wb * lambda;
}