动态 SDF 字体渲染方法
动态 SDF 字体 介绍
在 Unity 中, TextMeshPro 对文本使用有向距离场(Signed Distance Field, SDF) 算法,相比原本的 ttf 字体,使用了 SDF 的文本,在任意距离、缩放尺寸下,都能渲染出清晰的文本,而 ttf 则可能出现毛边,失真的情况,而且对一些文本效果:描边、阴影、外发光、内发光等,TextMeshPro 通过 Shader 实现,相比原生 Text 组件通过增加顶点偏移方式,渲染效果更好,效率也更高,NeoX 引擎中也内置了 SDF 字体支持。

字体渲染方式
BitmapFont
最简单的文本渲染方式是:点阵字体(Dot-matrix-fonts)也叫位图字体(Bitmap-fonts),即将用到的字符,预先输出到一张贴图中,使用的时候再找到对应的字符的 UV,再绘制文本。
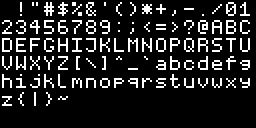
这种方法的缺点也很明显:字符集、字体的样式、字号在输出完贴图后就固定了
TureType Font
另外一个就是使用 FreeType 加载矢量字体(TrueType)来渲染文本。
- ttf:TrueType Font 是Apple公司和Microsoft公司共同推出的字体文件格式
- otf:OpenType Font 是 TTF 的升级版,而 OTF 是采用的是 PostScript 曲线,支持 OpenType 高级特性的更高级字体。
- ttc:TTC 就是几个 TTF 合成的字库,字库中的字体大部分字都一样,共享笔画数据,个别字符有差异。
字体文件中存放的是每个字符绘制的样条曲线控制点,可以使用Glyph Inspector(在线字形查看器)来查看对应 ttf 文件中字符的信息:

其中: contours 中每个 contour 都是首尾闭合的轮廓,这里 g 有两个轮廓组成(最外层的边缘,以及中间空心的 O 轮廓)。蓝色点表示边缘上的点,红色的点是样条曲线的控制点 1。
- 一红一蓝:绘制 2 次贝塞尔曲线
- 两蓝:绘制线段
- 两红:两个控制点的连线 与 曲线相交处(数学上可推导,该交点就是两个控制点连线的中点),会有个 隐藏曲线点,分成 两个 2次-贝塞尔曲线;(就是下面 有小数 0 .5 的 终点)
下图是字符 B 通过控制点绘制的过程:

下面是一段文本的渲染结果,蓝色的线表示每行的 x,y 轴线。

渲染上面文本,对应字体会生成一张纹理,如下图所示:

不同字号,斜体、粗体的字模光栅化后都会存储在字体贴图中,大致原理跟 Bitmap Font 类似,只是字符的贴图是通过加载矢量字体,动态增加到贴图中。
下图是 FreeType 加载矢量字体中一些参数,左图是横向排版,右图是竖向排版


- XY 轴:图中粗线是 XY 轴,其中远点是渲染该字符的局部原点(横向排版是 X 轴就是基线 baseline,竖向排版时,Y 轴是 baseline)
- width,height:是对应字符的长宽
- bearingX,bearingY:是字符渲染时,相对原点的偏移量
- advance:步进宽度,表示两个相邻字符之间的距离

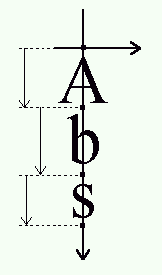
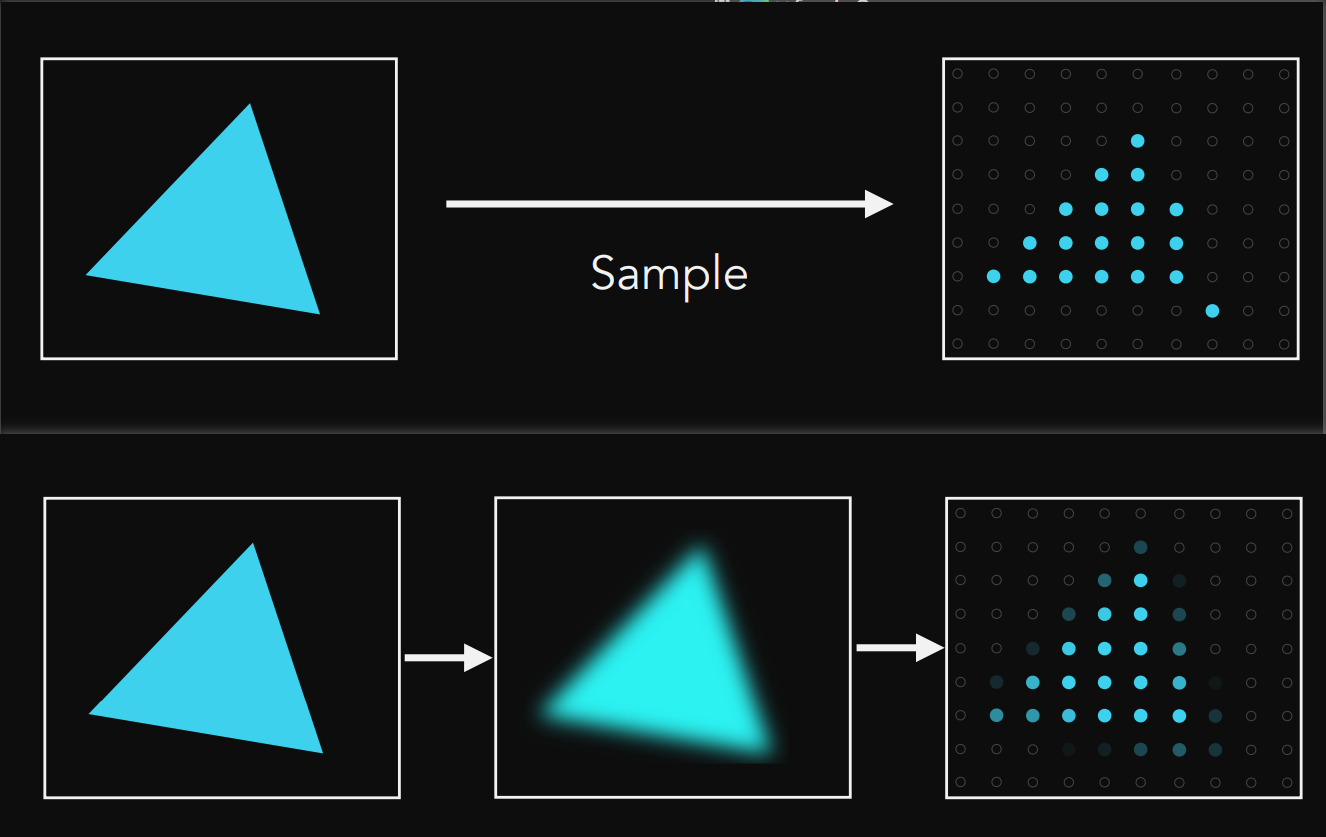
渲染时,需要根据文本字号,将 ttf 中的字符光栅化成对应的贴图:

左边是字体文件中的样条曲线,中间是不带抗锯齿光栅化结果,右边是带抗锯齿光栅化结果
光栅化的过程可以参考 game101 光栅化与抗锯齿
下图展示了光栅化的过程:上图是不带抗锯齿的版本,直接判断像素中心点是不是在三角形内
下图是抗锯齿版本,根据实际像素面积占比来计算颜色值(面积计算非常复杂,因此实际应用时会采用 MSAA,即将像素点拆分成四个小区域,分别判断这个四个小区域是不是在三角形内,来计算像素点的颜色占比)

SDF font
在贴图里面,不再存储纹理的像素数据,而是存储每一个点到边缘的距离:

这是字符 a 距离图,红色点表示边缘上的点,内部的像素点到边缘的最近距离为负值,外部的像素点到边缘最近的距离为正值。

其中 字符 a 灰度图如下(灰度表示该像素到字符边缘的距离,下面的图是距离标准化后的结果):

渲染时,采样贴图,将小于 0.5 的部分设置透明,即可还原最终的文本,下图是 DistanceMark 变化时 [0-1] 的渲染情况

Shader "Custom/SDF_Base"
{
Properties
{
_MainTex("Texture", 2D) = "black" {}
_DistanceMark("Distance Mark", Range(0,1)) = 0.5
_SmoothDelta("Smooth Delta", Range(0,0.02)) = 0.5
}
fixed4 frag(v2f i) : SV_Target
{
fixed4 col;
fixed4 sdf = tex2D(_MainTex, i.uv);
float distance = sdf.a;
col.a = smoothstep(_DistanceMark - _SmoothDelta, _DistanceMark + _SmoothDelta, distance);
col.rgb = lerp(fixed3(0,0,0), fixed3(1,1,1), col.a);
return col;
}
}smooth_func:用法

SDF 生成算法
生成 SDF 贴图的算法有很多包含:8SSEDT(8-point Signed Sequential Euclidean Distance Transform)应该是综合速度与错误率性价比最高的。另外可选的方案还有Chamfer3x3 DT(错误率稍高,速度稍快)或者4SSEDT(速度很快,错误率偏高)。
二值化算法
图形区域值为 1,图形区域外颜色值为 0,对于区域内的像素点,最近距离就是找到一个值为 0 的像素点,并且距离最近,区域外的类似。
- 暴力法:直接遍历整个图片(Width * Height),在像素附近(N*M)的区域内,找到该像素最近的边缘距离,复杂度(O(width * height * N * M)
find_range = 5
for i in range(pix_width):
for j in range(pix_height):
left = max(0, i - find_range)
right = min(pix_width, i + find_range)
top = max(0, j - find_range)
bottom = min(pix_height, j + find_range)
is_inside = (new_pic[i, j] == 1)
if dist_array[i, j] == 0:
continue
dist_array[i, j] = -max_int if is_inside else max_int
for i1 in range(left, right):
for j1 in range(top, bottom):
if is_inside:
if dist_array[i1, j1] == 0:
dist = -math.sqrt((i1 - i) ** 2 + (j1 - j) ** 2)
dist_array[i, j] = max(dist_array[i, j], dist)
else:
if dist_array[i1, j1] == 0:
dist = math.sqrt((i1 - i) ** 2 + (j1 - j) ** 2)
dist_array[i, j] = min(dist_array[i, j], dist)- 8SSEDT 算法
8SSEDT 的核心思想是:计算某一个像素的最近距离,可以通过它附近八个方向的邻近点来计算,$x_i, y_j$ 表示当前像素最近的目标点的偏移量
EDT:求解欧拉距离,两点距离 $\sqrt{(x_1 - x_2)2+(y_1-y_2)2}$
-1, 0)表示左边像素就是目标点
(1, 1) 表示右下角的像素点就是目标点
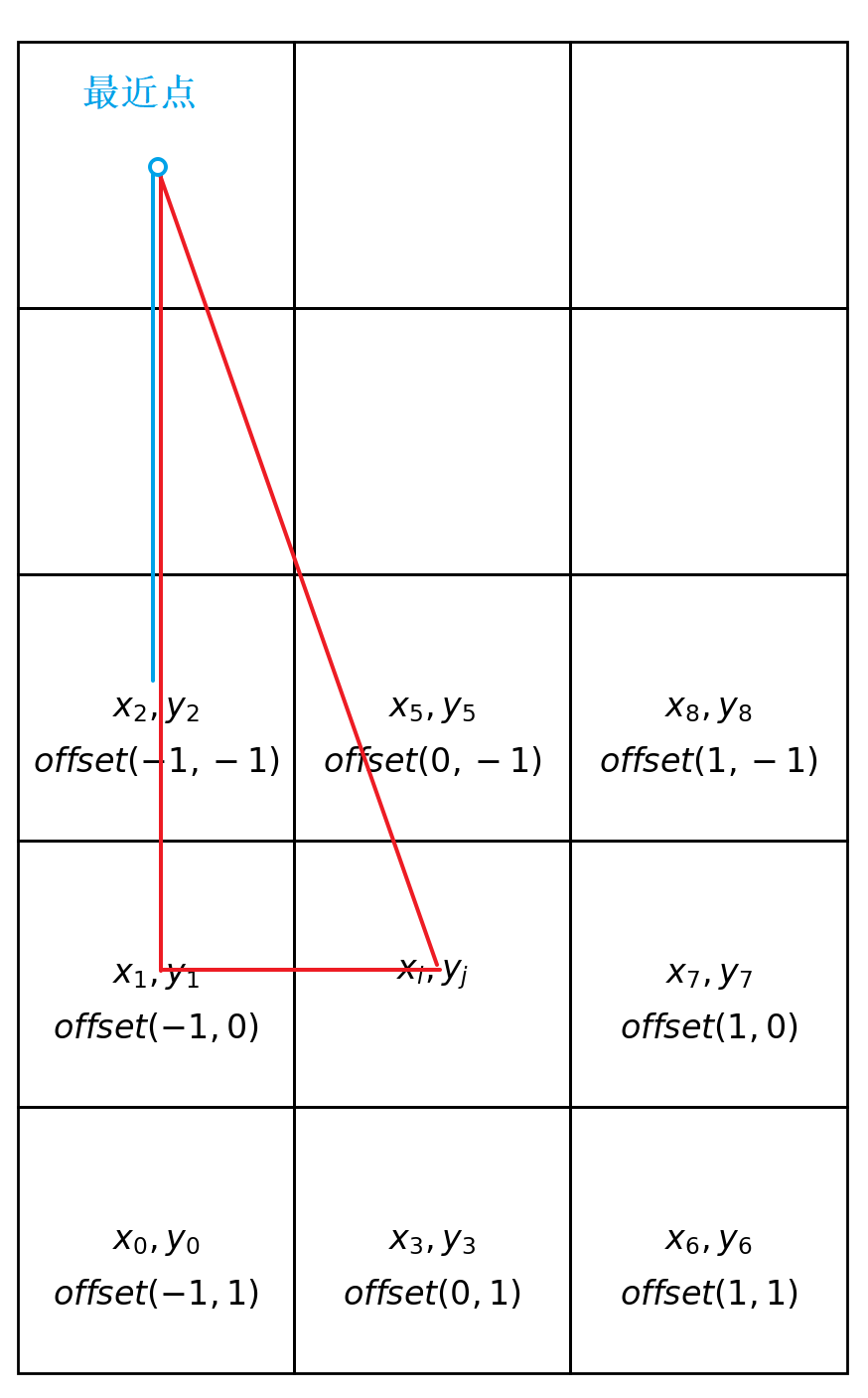
如上图所示,$x_2, y_2$ 到最近点的偏移值为 $(0, 2)$,则可以得出当前点最近距离为斜边长,其他7个方向类似,求出最小距离。
事实上,对八个方向的遍历分为两个 PASS(为了确保对应方向上邻居的值已经计算完毕)
- PASS0:从左上角开始遍历,逐行遍历,每次计算左上方的四个方向
- PASS1:从右下角开始遍历,逐行遍历,每次计算右下方的四个方向
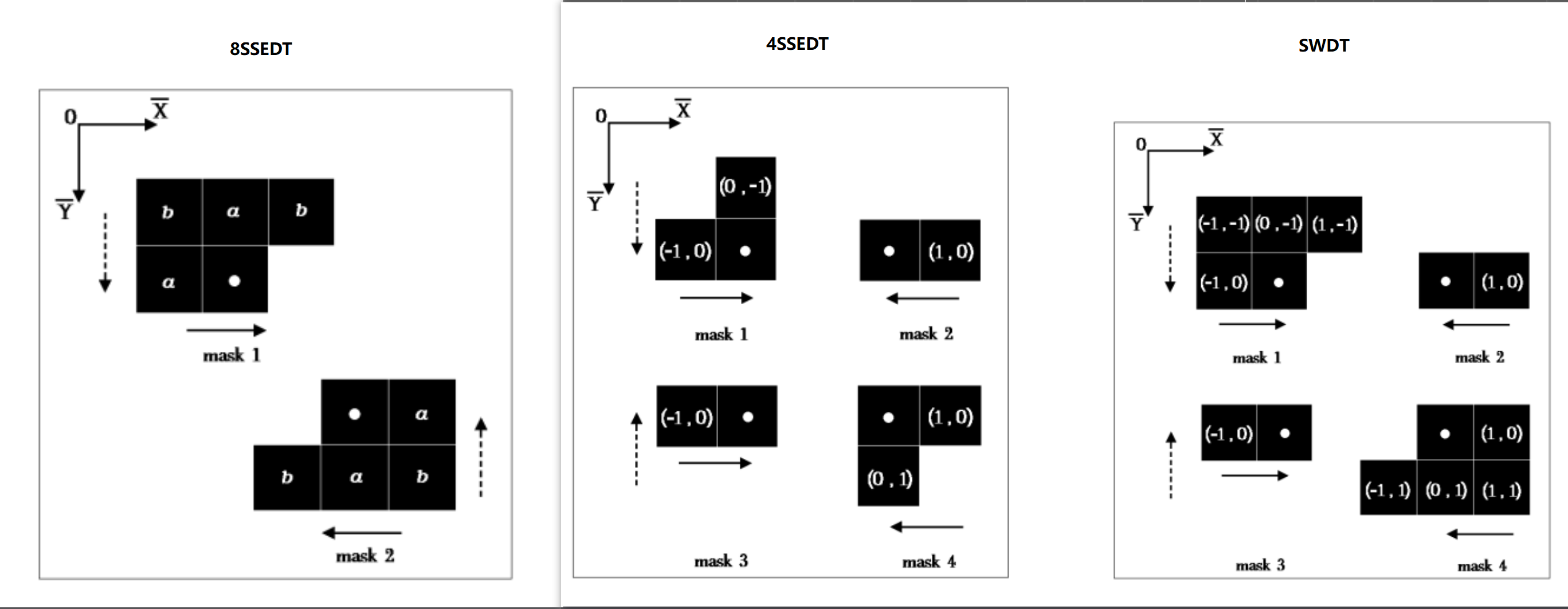
上图表示 8SSEDT,4SSEDT,以及SWDT 的扫描方式,图中的 mask 就一个 PASS,8SSEDT扫描方式会分为两个 PASS 进行(左上角 PASS0, 右下角 PASS1, 打点的方块是当前计算点,周围的黑色方块表示当前 PASS 需要计算的临近像素),最右图是 SEDT 算法的扫描方式,在 8SSEDT 基础上多了mask 2 和 3(在PASS0 做完后增加 PASS2 对该行再扫描一次),但是为了要求得正确的欧几里得距离,这两步必须的,没有这两步会导致斜线方向上的距离计算出现误差,详细可以参考论文链接。
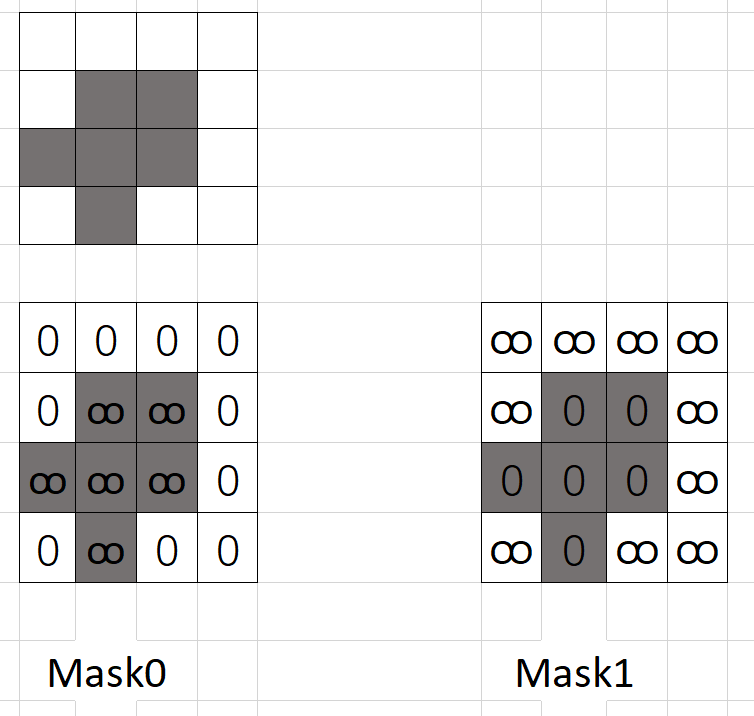
并且会使用两个通道 Mask,分别计算物体内到目标点距离,跟物体外到目标点的距离,每个 Mask 初始化时,会根据当前图片的灰度值,转成二值化图(灰度大于128 表示物体内,小于128 的丢弃),并初始化对应的 Mask,举个例子,下面是一个目标图,黑色表示物体内,白色表示物体外,初始化两个 Mask 如下图所示:
Mask1 经过一次遍历后结果如下(两次遍历结合起来,就能求出所有像素当目标点的最短距离)
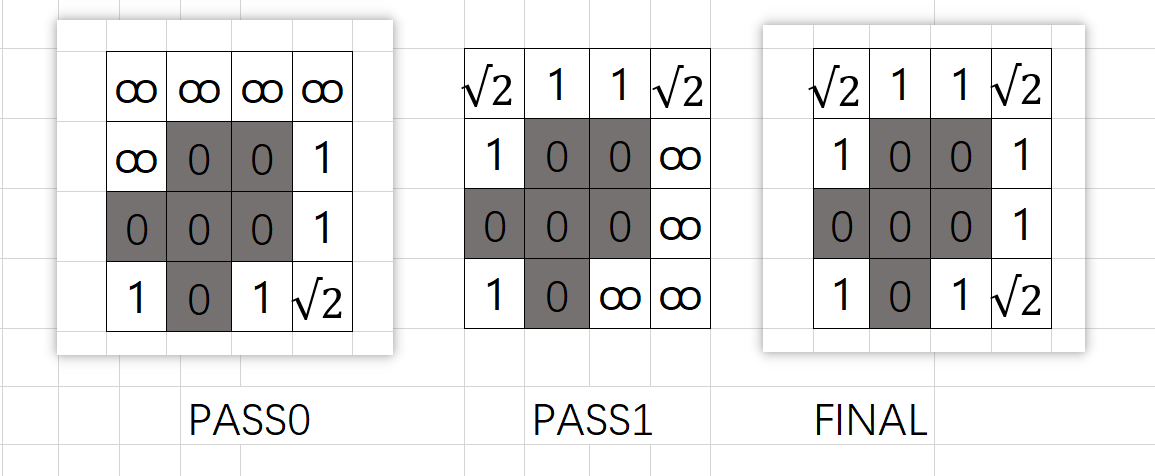
最后将两次计算结果相减,即可得出最终结果 $Mask_1 - Mask_0$。详细代码
struct Point
{
int dx, dy;
int DistSq() const { return dx*dx + dy*dy; }
};
struct Grid
{
Point grid[HEIGHT][WIDTH];
};
/// 根据灰度继续二值化,并初始化两个 Mask
if ( g < 128 )
{
// inside = Point(0, 0)
// empty = Point(99999999, 99999999)
Put( grid1, x, y, inside );
Put( grid2, x, y, empty );
} else {
Put( grid2, x, y, inside );
Put( grid1, x, y, empty );
}
// Generate the SDF.
GenerateSDF( grid1 );
GenerateSDF( grid2 );
// 比较当前距离跟邻居距离
void Compare( Grid &g, Point &p, int x, int y, int offsetx, int offsety )
{
Point other = Get( g, x+offsetx, y+offsety );
other.dx += offsetx;
other.dy += offsety;
if (other.DistSq() < p.DistSq())
p = other;
}
void GenerateSDF( Grid &g )
{
// Pass 0
for (int y=0;y<HEIGHT;y++)
{
for (int x=0;x<WIDTH;x++)
{
Point p = Get( g, x, y );
// 左 上 左上 右上 方向
Compare( g, p, x, y, -1, 0 );
Compare( g, p, x, y, 0, -1 );
Compare( g, p, x, y, -1, -1 );
Compare( g, p, x, y, 1, -1 );
Put( g, x, y, p );
}
for (int x=WIDTH-1;x>=0;x--)
{
Point p = Get( g, x, y );
Compare( g, p, x, y, 1, 0 );
Put( g, x, y, p );
}
}
// Pass 1
for (int y=HEIGHT-1;y>=0;y--)
{
for (int x=WIDTH-1;x>=0;x--)
{
Point p = Get( g, x, y );
// 右 下 左下 右下
Compare( g, p, x, y, 1, 0 );
Compare( g, p, x, y, 0, 1 );
Compare( g, p, x, y, -1, 1 );
Compare( g, p, x, y, 1, 1 );
Put( g, x, y, p );
}
for (int x=0;x<WIDTH;x++)
{
Point p = Get( g, x, y );
Compare( g, p, x, y, -1, 0 );
Put( g, x, y, p );
}
}
}灰度图
直接使用二值化图片生成 SDF 在图像边缘会有一些误差,详细参看论文链接,如下图:

使用二值化图,则图 c 中 B 点在计算距离时,A,C 像素灰度不够(小于0.5),会被丢弃,最终计算的距离方向是虚线箭头所示,但是真实的距离方向应该是实线箭头。
因此,对于边缘的像素($0 <$ 灰度 $< 1 $)需要单独处理,按照论文里个方法,对边缘上的像素进行分类:
- 边缘垂直或者平行穿过像素
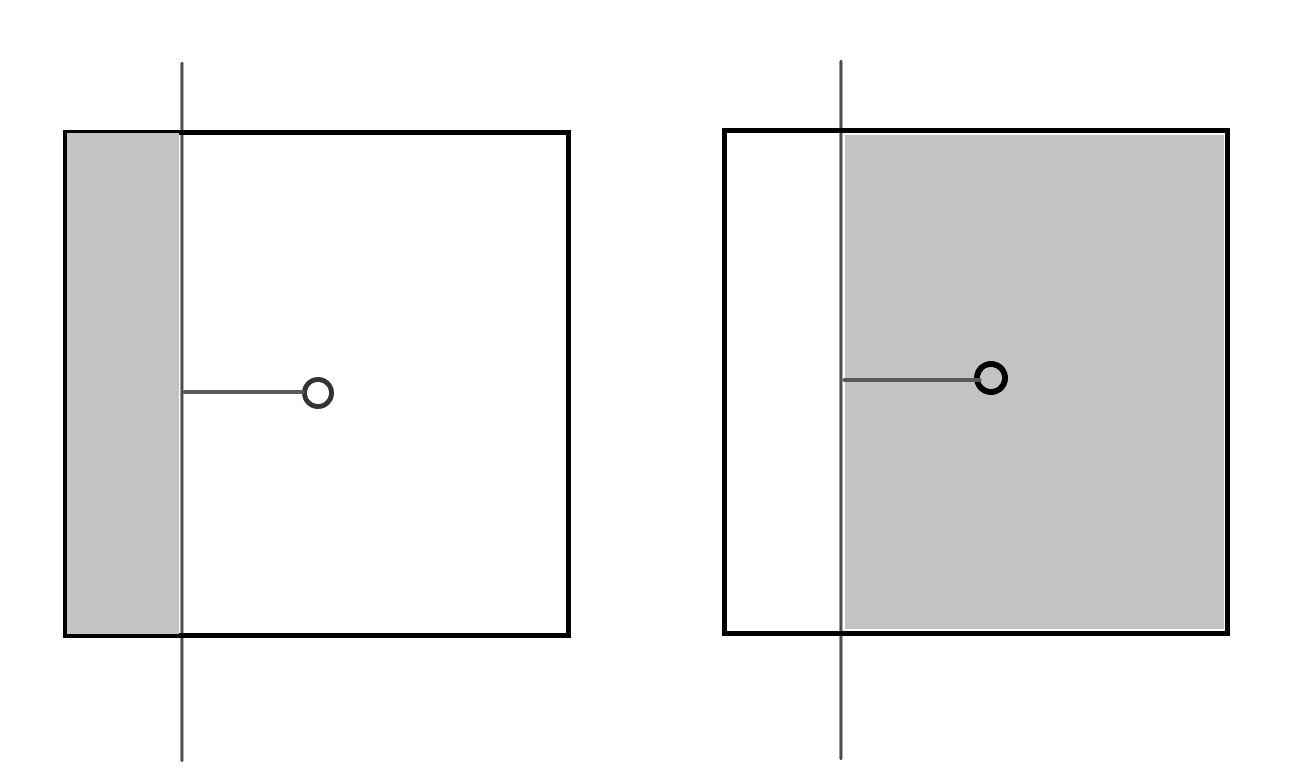
$$d_f = 0.5 - a$$
其中:
$d_f$:距离
a:像素灰度值
- 边缘斜着穿过像素
如下图(边缘的斜率可能不一样,但是都可以通过下面的图做旋转得到类似的结果)
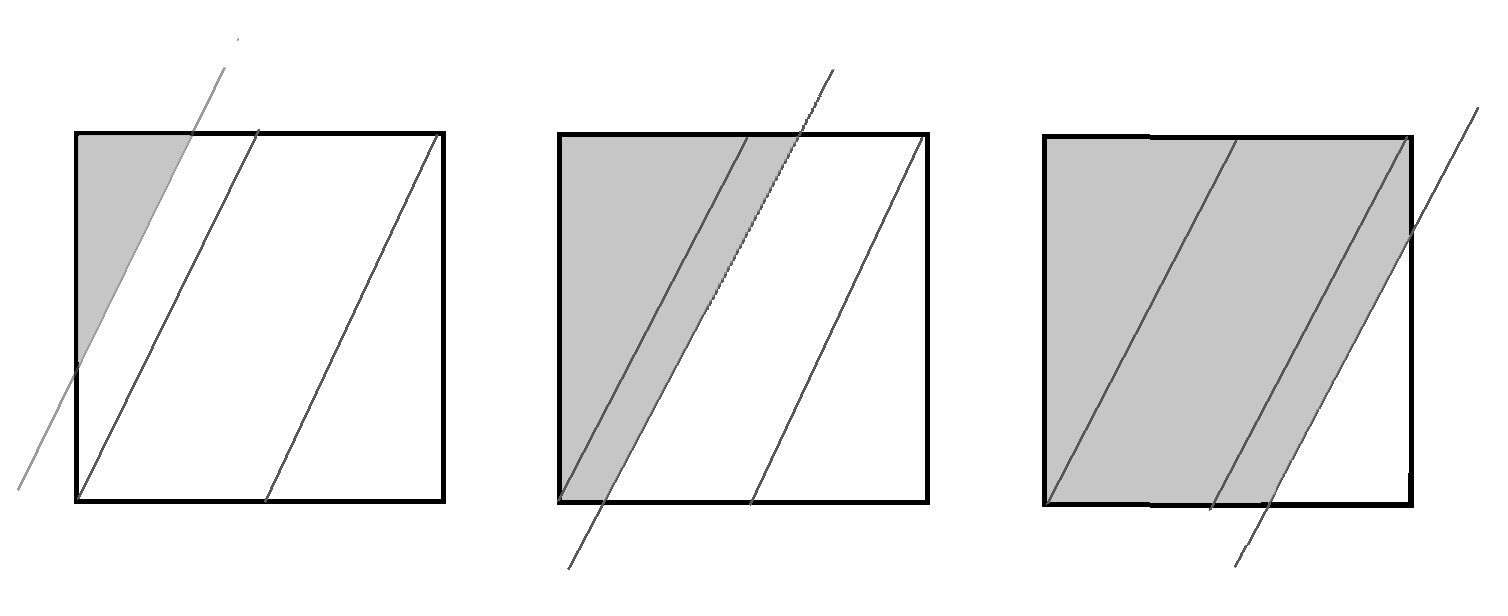
灰色的地方表示目标像素灰度
首先定义几个常量:
$a_1$: 边缘穿过像素点左边的区域,并且经过像素最边缘的点
$a_2$: 中间区域
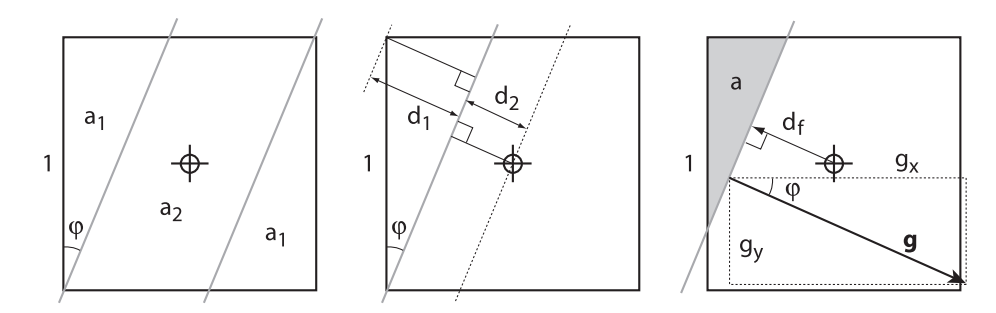
由上图左(1) 跟 左(2) 可求出下面几个常量:
$$\begin{align}
a_1 &= tan \varphi = \frac{g_y}{g_x} \
a_2 &= 1 - 2a_1 \
d_1 &= sin \varphi = g_y \
d_2 &= \frac{1}{\sqrt{2}}sin (\frac{\pi}{4} - \varphi) = \frac{1}{\sqrt{2}}sin (\frac{\pi}{4} - arcsin(g_y))
\end{align}
$$
其中单位向量 $\vec{g} = (g_x, g_y) = (cos \varphi, sin \varphi)$
则斜着穿过像素的情况有如下几种
- $a < a_1$
- $a_1 \leq a < a_1+a_2$
- $a_1+a_2 \leq a < 1$
直接引用论文中的结论:
$$d_f =
\begin{cases}
\frac{(g_x + g_y)}{2} - \sqrt{2g_xg_ya} & 0 \leq a \leq a_1 \
(0.5 - a)g_x & a_1 \leq a \leq 1-a_1 \
-\frac{(g_x + g_y)}{2} - \sqrt{2g_xg_y(1-a)} & 1-a_1 \leq a \leq 1
\end{cases}
$$
梯度算子
最终我们需要求出 $\vec{g}$ 就可以得出最终结果 $d_f$,而 $\vec{g}$ 是像素边缘的梯度,论文里没有说怎么求,但是图像处理中,提供了多种梯度算子来计算边缘梯度。首先介绍下梯度:
一维连续数集上的函数的斜率公式:
$$f’(x) = f(x + \Delta x) - f(x)$$
二维连续数集上函数偏导数:
$$
\begin{aligned}
\frac{\partial f(x, y)}{\partial x} &= f(x + \Delta x, y) - f(x, y) \
\frac{\partial f(x, y)}{\partial y} &= f(x, y + \Delta y) - f(x, y) \
\end{aligned}
$$
对于图像来说,是一个二维的离线型数集,因此推广二维连续型求函数偏导的方法,来求图像的偏导数,即在 $(x,y)$ 处的最大变化率,也就是梯度。
$$\begin{aligned}
g_x &= \frac{\partial f(x, y)}{\partial x} = f(x + 1, y) - f(x,y) \
g_y &= \frac{\partial f(x, y)}{\partial x} = f(x, y + 1) - f(x,y) \
\end{aligned}
$$
把图片取像素点值的操作当成函数 $f(x,y)$,$\Delta$ 量为整数,且最小变化量为 1 个像素点
因此
$$\nabla f \equiv grad(f) = [g_x, g_y]^T = \left[\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right]^T$$
最后得出的模板如下:
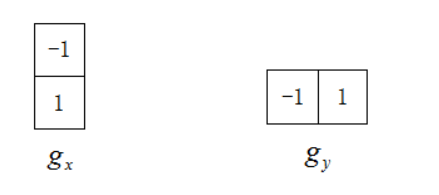
上面是考虑水平跟竖直方向上的梯度
Roberts 算子
对角线方向的梯度:
$$\begin{aligned}
g_x &= \frac{\partial f(x, y)}{\partial x} = f(x + 1, y + 1) - f(x, y) \
g_y &= \frac{\partial f(x, y)}{\partial x} = f(x + 1, y) - f(x, y + 1) \
\end{aligned}
$$

3*3 模板
2*2 大小的模板在概念上很简单,但是他们对于用关于中心店对称的模板来计算边缘方向时,不是很有用,因此一般会使用 3 * 3 模板
- Prewitt 算子
水平竖直方向以及对角线方向的 $G_x$, $G_y$
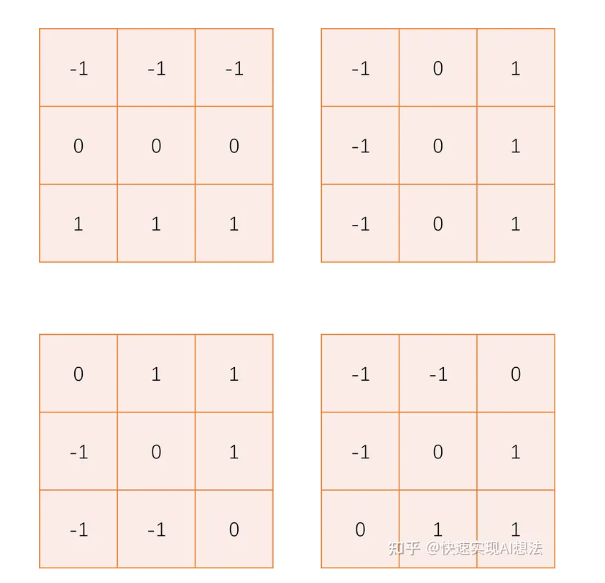
- Sobel 算子
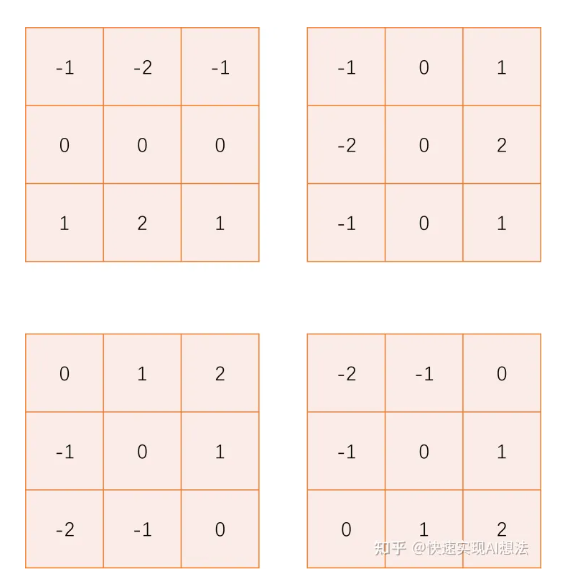
- Isotropic 算子
$$G_x = \left[
\begin{matrix}
-1 \quad 0 \quad 1 \
-\sqrt{2} \quad 0 \quad \sqrt{2} \
-1 \quad 0 \quad 1
\end{matrix} \
\right] * A \qquad G_y = \left[
\begin{matrix}
-1 \quad -\sqrt{2} \quad -1\
0 \quad 0 \quad 0\
1 \quad \sqrt{2} \quad 1
\end{matrix}
\right] * A$$
如果图片为 A
$$A=\left[
\begin{matrix}
P_1 \quad P_2 \quad P_3\
P_4 \quad P_5 \quad P_6\
P_7 \quad P_8 \quad P_9
\end{matrix}
\right]$$
$$G=\sqrt{G_x^2 + G_y^2}$$
$$
G_x = P_3-P_1+\sqrt{2}(P_6-P_4) + P_9 - P_7
$$
$$
G_y = P_7-P_1+\sqrt{2}(P_8-P_2) + P_9 - P_3
$$
$$
\quad\
g_x = \frac{G_x}{G}\
\quad\
g_y = \frac{G_y}{G}
$$
代码实现
下面给出完整的 python 代码的实现
import math
import numpy as np
from PIL import Image
def color_2_gray(color):
r, g, b = color[0], color[1], color[2]
gray = 0.2989 * r + 0.5870 * g + 0.1140 * b
return gray / 255.0
## 线性插值方法这里将一张 1024 * 1024 的大图,插值成 32 * 32,灰度图
## 然后再计算 SDF 距离
def bilinear_interpolation(image, out_width, out_height, corner_align = True):
width, height = image.width, image.height
output_image = np.zeros((out_height, out_width))
scale_x_corner = float(width - 1) / (out_width - 1)
scale_y_corner = float(height - 1) / (out_height - 1)
scale_x = float(width) / out_width
scale_y = float(height) / out_height
for out_x in range(out_width):
for out_y in range(out_height):
if corner_align:
x = out_x * scale_x_corner
y = out_y * scale_y_corner
else:
x = (out_x + 0.5) * scale_x - 0.5
y = (out_y + 0.5) * scale_y - 0.5
x = np.clip(x, 0, width - 1)
y = np.clip(y, 0, height - 1)
x0, y0 = int(x), int(y)
x1, y1 = x0 + 1, y0 + 1
if x0 == width - 1:
x0 = width - 2
x1 = width - 1
if y0 == height - 1:
y0 = height - 2
y1 = height - 1
xd = x - x0
yd = y - y0
p00 = color_2_gray(image.getpixel((x0, y0)))
p01 = color_2_gray(image.getpixel((x1, y0)))
p10 = color_2_gray(image.getpixel((x0, y1)))
p11 = color_2_gray(image.getpixel((x1, y1)))
x0y = p01 * xd + p00 * (1 - xd)
x1y = p11 * xd + p10 * (1 - xd)
value = x1y * yd + x0y * (1 - yd)
output_image[out_y, out_x] = 1 - value
return output_image
class Point(object):
def __init__(self):
self.alpha = 0
self.gx = 0
self.gy = 0
self.dx = 0
self.dy = 0
self.df = 0
self.di = 0
self.distance = 0
class OctSSEDT(object):
def __init__(self):
pass
## img 是一张 1024 * 1024 的字体图
def calc3_3AAEDT(self, img, pix_per_pix):
width = img.width
height = img.height
out_width = int(width / pix_per_pix)
out_height = int(height / pix_per_pix)
out_img = bilinear_interpolation(img, out_width, out_height)
value_min = out_img.min()
for i in range(out_width):
out_img[i, 0] = value_min
out_img[i, out_width - 1] = value_min
for i in range(out_height):
out_img[0, i] = value_min
out_img[out_height - 1, i] = value_min
value_max = out_img.max()
value_min = out_img.min()
for i in range(out_height):
for j in range(out_width):
color = out_img[i, j]
color = (color - value_min) / (value_max - value_min)
if color < 1e-5:
color = 0
if color > 0.99999:
color = 1
out_img[i, j] = color
out_dist = {}
in_dist = {}
self.img = out_img
self.generate_sdf(in_dist, 0)
self.generate_sdf(out_dist, 1)
scale = 255 / ((5 + 1) * 2) * 2
for j in range(out_height):
for i in range(out_width):
p0 = in_dist[(i, j)]
p1 = out_dist[(i, j)]
d0 = p0.distance
d1 = p1.distance
df0 = p0.df
df1 = p1.df
# out_img[i, j] = math.sqrt(p1.di) - math.sqrt(p0.di)
if d0 < d1:
d1 = math.sqrt(p1.di) + p1.df
d = max(0, min(127.5, d1 * scale))
out_img[i, j] = (127.5 - d + 0.5) / 255
else:
d0 = math.sqrt(p0.di) + p0.df
d = max(0, min(127.5, d0 * scale))
out_img[i, j] = (127.5 + d + 0.5) / 255
return out_img
## 应用 Isotropic 算子
def calc_edge_gradient(self, index_x, index_y, point):
img = self.img
width, height = img.shape[0], img.shape[1]
gx = 0
gy = 0
sqrt2 = 1.41421356
gxy_offset = [
(-1, -1), (0, -1), (1, -1),
(-1, 0), (0, 0), (1, 0),
(-1, 1), (0, 1), (1, 1),
]
gx_matrix = [
-1, 0, 1,
-sqrt2, 0, sqrt2,
-1, 0, 1,
]
gy_matrix = [
-1, -sqrt2, -1,
0, 0, 0,
1, sqrt2, 1,
]
for i in range(9):
offset = gxy_offset[i]
x = index_x + offset[0]
y = index_y + offset[1]
if x < 0 or x >= width or y < 0 or y >= height:
continue
img_value = img[x, y]
gx_m = gx_matrix[i]
gy_m = gy_matrix[i]
gx += gx_m * img_value
gy += gy_m * img_value
g = math.sqrt(gx * gx + gy * gy)
if g > 0:
gx /= g
gy /= g
point.gx = gx
point.gy = gy
## 计算边缘像素的距离(论文中的方法)
def calcEdgeDistance(self, gx, gy, a):
img = self.img
width, height = img.shape[0], img.shape[1]
df = 0
if gx == 0 or gy == 0:
return 0.5 - a
g = math.sqrt(gx * gx + gy * gy)
gx = abs(gx / g)
gy = abs(gy / g)
if gx < gy:
t = gx
gx = gy
gy = t
a1 = gy / gx
if a >= 0 and a <= a1:
df = (gx + gy) / 2 - math.sqrt(2 * gx * gy * a)
elif a <= 1 - a1:
df = (0.5 - a) * gx
else:
df = -(gx + gy) / 2 + math.sqrt(2 * gx * gy * (1 - a))
return df
def compare_dist(self, dist, point, x, y, offset_x, offset_y):
img = self.img
width, height = img.shape[0], img.shape[1]
width, height = img.shape[0], img.shape[1]
maxDistance = width * width + height * height
if x + offset_x < 0 or x + offset_x >= width
or y + offset_y < 0 or y + offset_y >= height:
return
other = dist[(x + offset_x, y + offset_y)]
if other.distance == maxDistance:
return
dx = other.dx + offset_x
dy = other.dy + offset_y
alpha = dist[x + dx, y + dy].alpha
df = self.calcEdgeDistance(dx, dy, alpha)
di = dx * dx + dy * dy
distance = di + df
if distance < point.distance:
point.distance = distance
point.dx = dx
point.dy = dy
point.df = df
point.di = di
## 8ssedt
def generate_sdf(self, dist, mask = 0):
img = self.img
width, height = img.shape[0], img.shape[1]
maxDistance = width * width + height * height
for j in range(height):
for i in range(width):
color = img[i, j]
point = Point()
point.alpha = color if mask == 1 else 1 - color
dist[(i, j)] = point
if point.alpha > 0.001 and point.alpha < 1:
self.calc_edge_gradient(i, j, point)
df = self.calcEdgeDistance(point.gx, point.gy, point.alpha)
point.dx = 0
point.dy = 0
point.df = df
point.di = 0
point.distance = df
continue
elif point.alpha == 0:
point.df = 0
point.di = maxDistance
point.distance = maxDistance
elif point.alpha == 1:
point.dx = 0
point.dy = 0
point.df = 0
point.di = 0
point.distance = 0
continue
self.compare_dist(dist, point, i, j, 0, -1)
self.compare_dist(dist, point, i, j, -1, 0)
self.compare_dist(dist, point, i, j, -1, -1)
self.compare_dist(dist, point, i, j, 1, -1)
for i in range(width - 1, -1, -1):
for j in range(height - 1, -1, -1):
point = dist[(i, j)]
if (point.alpha > 0 and point.alpha < 1) or point.distance == 0:
continue
self.compare_dist(dist, point, i, j, 0, 1)
self.compare_dist(dist, point, i, j, 1, 0)
self.compare_dist(dist, point, i, j, 1, 1)
self.compare_dist(dist, point, i, j, -1, 1)