实时阴影技术

发表于 分类于 阅读次数： 本文字数： 11k 阅读时长 ≈ 10 分钟

硬阴影

对于点光源来说，它只会产生硬阴影。

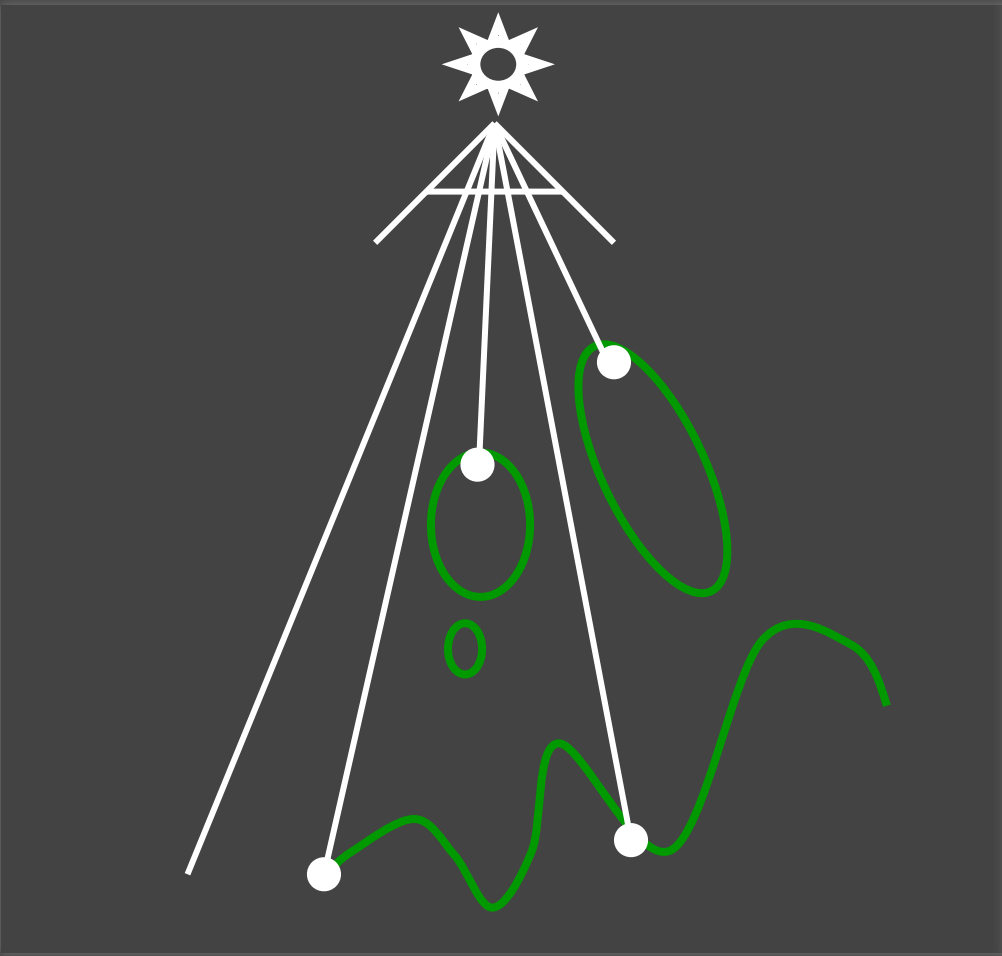
shadow maping 基本原理

点光源的 Shadow Map 算法，分为两个 PASS

  • PASS 0：从光源位置看向场景，并且计算出光源到能看到的最近的物体的深度图，并将深度存起来作为 Shadow Map
// shadowVertex.glsl
// ...
void main(void) {
  vNormal = aNormalPosition;
  vTextureCoord = aTextureCoord;
  gl_Position = uLightMVP * vec4(aVertexPosition, 1.0);
}
// shadowFragment.glsl
// ...
void main(){
  // 将 z 拆分到 4 个通道存储
  gl_FragColor = pack(gl_FragCoord.z);
}

如下图， Shadow Map 记录了 Light Camera 所看到的最近的深度图，颜色越深，离相机越近

  • PASS 1：然后第二个 PASS 从相机出发，使用第一个 PASS 得到的 Shadow map，去判断渲染的像素点，是否在阴影中（计算当前点到光源距离，跟 Shadow map 中采样的深度作比较），最终计算得出 Visibility（0 or 1）

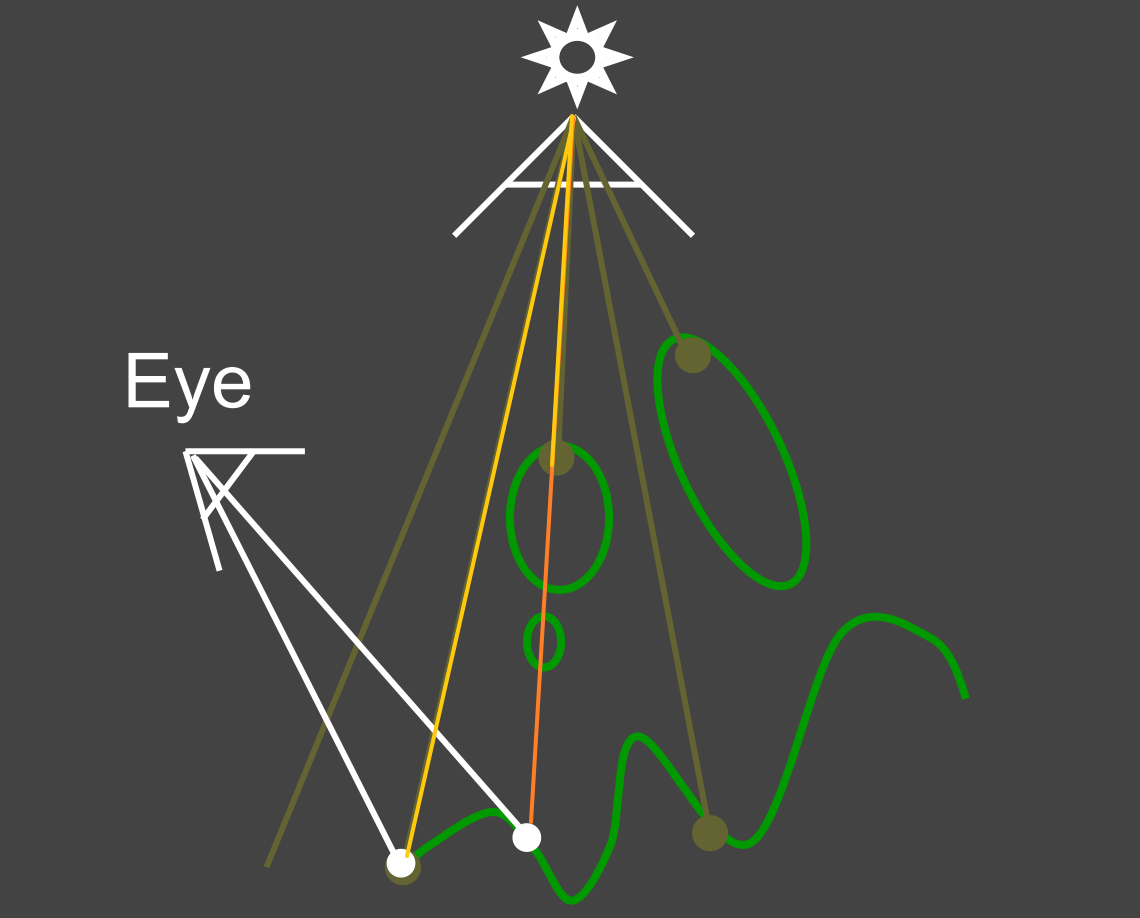
太阳 表示灯光位置，绿色线 表示场景中的物体
右图中，第一个点计算得出的数值跟阴影图中数据一致
右图中，第二个点计算出来的距离比阴影贴图中的大，因此改点在阴影里

// phongVertex.glsl
// ...
void main(void) {
  vNormal = (uModelMatrix * vec4(aNormalPosition, 0.0)).xyz;
  vTextureCoord = aTextureCoord;
  vFragPos = (uModelMatrix * vec4(aVertexPosition, 1.0)).xyz;
  vPositionFromLight = uLightMVP * vec4(aVertexPosition, 1.0);
  gl_Position = uProjectionMatrix * uViewMatrix * uModelMatrix
    * vec4(aVertexPosition, 1.0);
}
// phongFragment.glsl 
// ...
void main(){
    // 归一化坐标
    vec3 projCoords = vPositionFromLight.xyz / vPositionFromLight.w;
    vec3 shadowCoord = projCoords * 0.5 + 0.5;
    // Shadow  1.0 表示没有阴影 0 表示阴影
    float visibility = 1.0;
    
    //将rgba四通道（32位）的值unpack成float类型的数值
    float depthInShadowmap = unpack(texture2D(shadowMap,shadowCoord.xy).rgba); 
    if(depthInShadowmap < shadowCoord.z){
        visibility = 0.0;
    }
    // blinnPhong光照着色
    vec3 color = blinnPhong();
    
    gl_FragColor = vec4(color * visibility, 1.0);
}

缺点

传统的 Shadow Map 技术存在一些缺陷：

自遮挡（Shadow Ance）

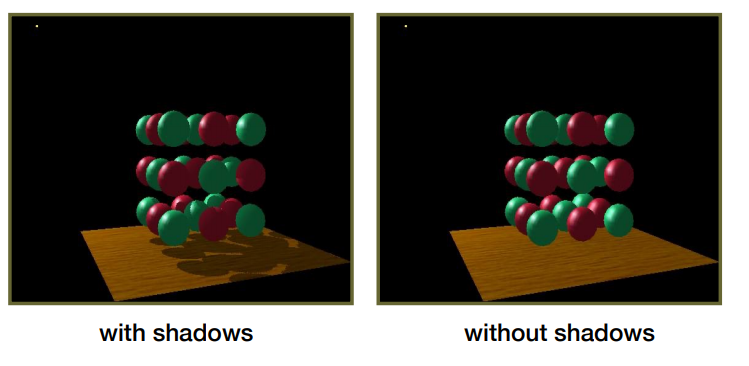
传统的 Shadow Map 存在由数值精度造成的自遮挡问题，即在下图中看到的地面上的不正确的纹路：

这是因为 shadow map 的分辨率太低。因为 shadow map 贴图的分辨率过低，阴影贴图的一个纹素会对应多个像素，而这些像素在shadow map空间中的深度是不同的，因此就会出现自己遮挡自己的情况，当光照与投影面垂直时，几乎不存在自遮挡现象，当光照向与平面接近平行时，平面会产生严重的自遮挡现象。

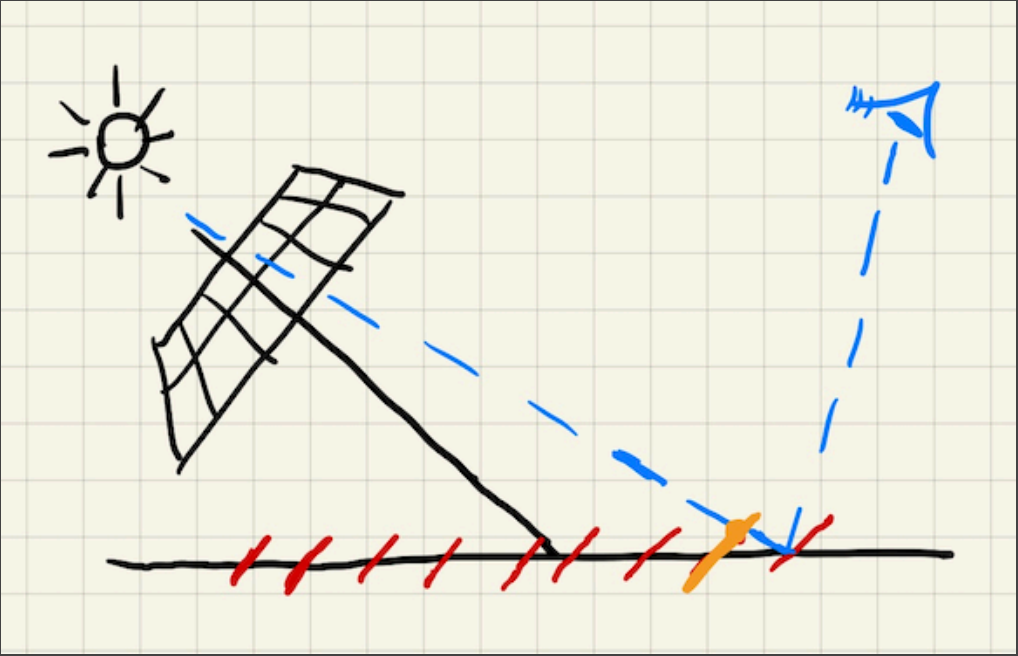
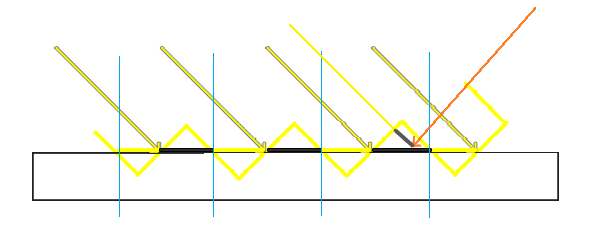
每个蓝色线隔开的地方，计算出来的深度一样，用黄色线条表示，但实际上，靠右侧的实际深度要大一些，因此，计算是否可见时，就容易出现自遮挡。（橙色箭头所示，实际深度还要加上灰色线段部分，如上图）

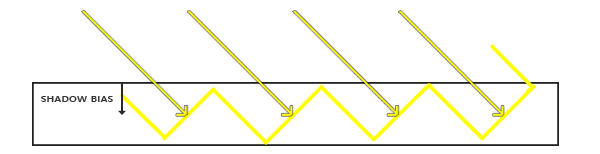
增加一个偏移值

最简单的方法就是，直接给采样阴影深度增加一个偏移值：相当于是把阴影深度往远处加，从而不容易产生自遮挡）。

// phongFragment.glsl
//...
void main(){
    // ...

    // Shadow
    float visibility = 1.0;
    // BIAS 调很大，为了显示漏光 bug
    const float BIAS = 0.01;

    //// 增加了 BIAS
    if(depthInShadowmap + BIAS < shadowCoord.z) {
        visibility = 0.0;
    }
    // ...
}

可以看到，自遮挡问题解决了，但是因为增加了 Bias，可能导致影子悬空。（Peter Panning 现象在物体缝隙间漏光，特别是遮挡物厚度小于 Bias 时）

Peter Pan 是童话故事里的彼得潘，他是个会飞的男孩，而 panning 有平移、悬浮之意

有另外一种跟 Bias 不太一样的方法（实际上原理相同）

  1. 不使用 Bias
  2. 第一个 Pass 设置成仅渲染背面（正面剔除），对于有厚度的物体，相当于是增加了遮挡物渲染后的深度大小

本来深度值应该是正方块上表面的距离，使用正面剔除后，深度值是正方块的下表面的距离了

  • 解决办法：避免使用单薄的几何体
动态 Bias

通过之前的介绍，使用过大的 Bias 增加深度的方法会导致影悬空问题，而过小的 Bias 又解决不了自遮挡问题，自遮挡问题产生又跟光线的角度有关系，因此可以采取根据平面倾角来自适应 Bias

float MIN_BIAS = 0.005;
float BIAS = 0.05;
float bias = max(BIAS * (1.0 - dot(normal, lightDir)), MIN_BIAS);
第二深度法

第二种解决办法是在计算光照方向的深度时，同时计算得到最小深度以及第二小的深度，然后用这两个的中间值作为最终深度存放到 Shadow Map 中

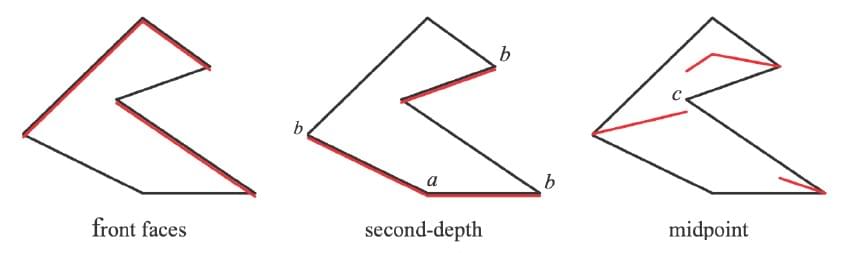
如上图所示，需要两个 PASS 来生成阴影贴图，第一个 PASS 设置背面剔除，第二个 PASS 设置为前向面剔除，这样就能分别获得两个深度，最后得出平均深度

但是这种方法要求遮挡物（投射阴影的物体）必须是闭合曲面（watertight），必须有正反面，然后会多增加一个 PASS 带来更大的开销，因此没有得到广泛应用。

锯齿

第二个缺点就是生成的 Shadow Map 分辨率是有限的，如果阴影面积过大，就会产生锯齿（Aliasing）

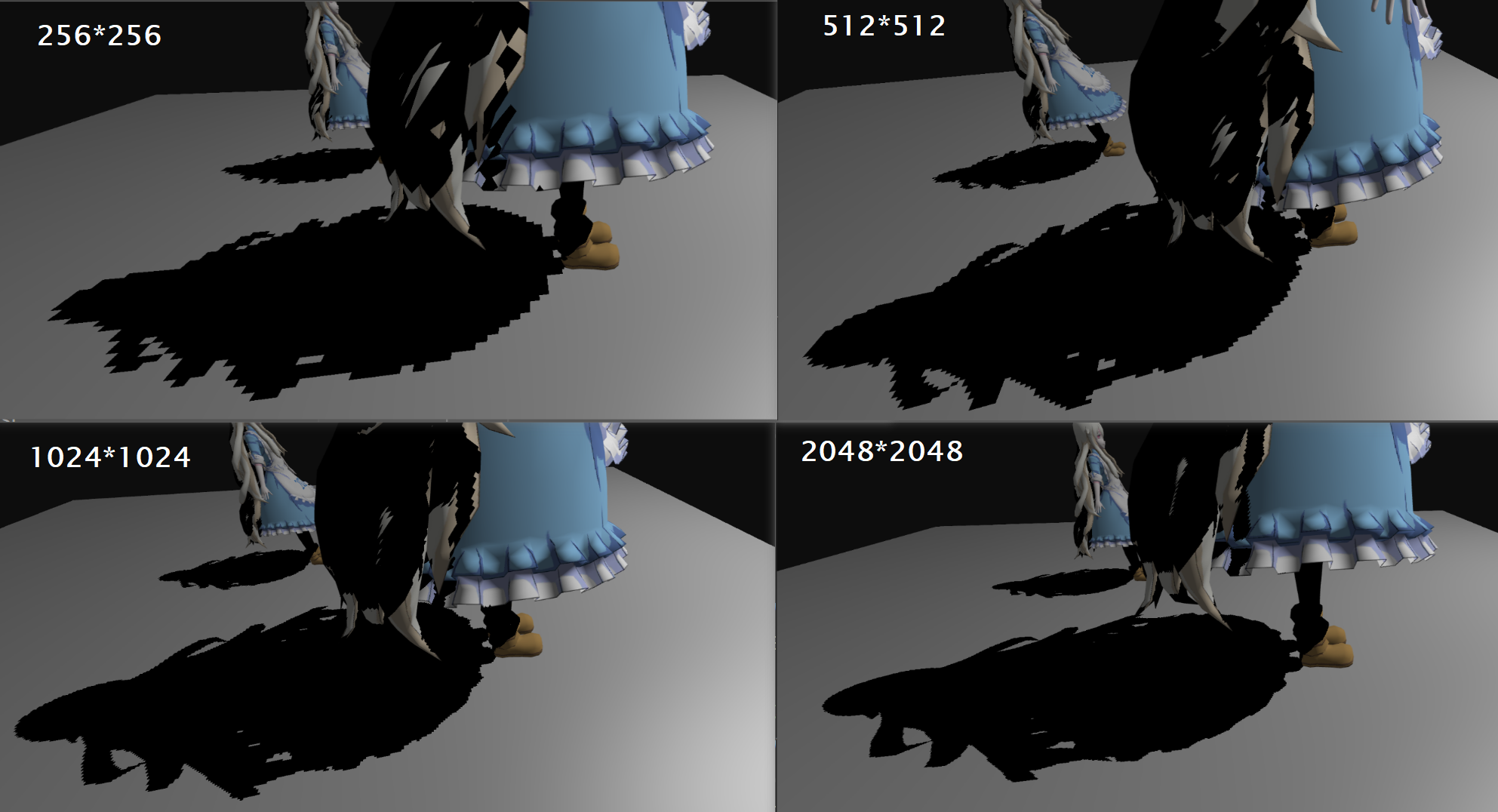
级联阴影贴图 CSM（Cascade Shadow Map）

当 Shadow Mapping 应用在大型场景中时，一张正常分辨率大小（如1024×1024）的贴图用来记录整个大型场景的阴影深度信息是非常不精确的，尤其是在靠近主摄像机的地方所看到的阴影将是严重失真的（一块块栅格）。

CSM 的思想是使用多层 Shadow Map 将视锥按照距离划分成多个阴影区，相机附近提供更高分辨率的深度纹理，而在远处提供更低分辨率的纹理，来帮助解决走样问题。

PCF (Percentage closer filtering)

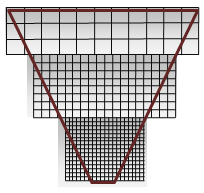
之前使用的 Shadow Maping 技术中，进行深度比较时，只对阴影贴图采样一次作比较，PCF 算法为了解决锯齿问题，采样时会在 对应点周围一定范围的像素 (例如下图 5*5) 进行多重采样，然后把采样区域内所有像素深度比较后的结果求平均得出最后的值，因此得出的 Visibility 不在是非 0 即 1，而是带有渐变的取值。

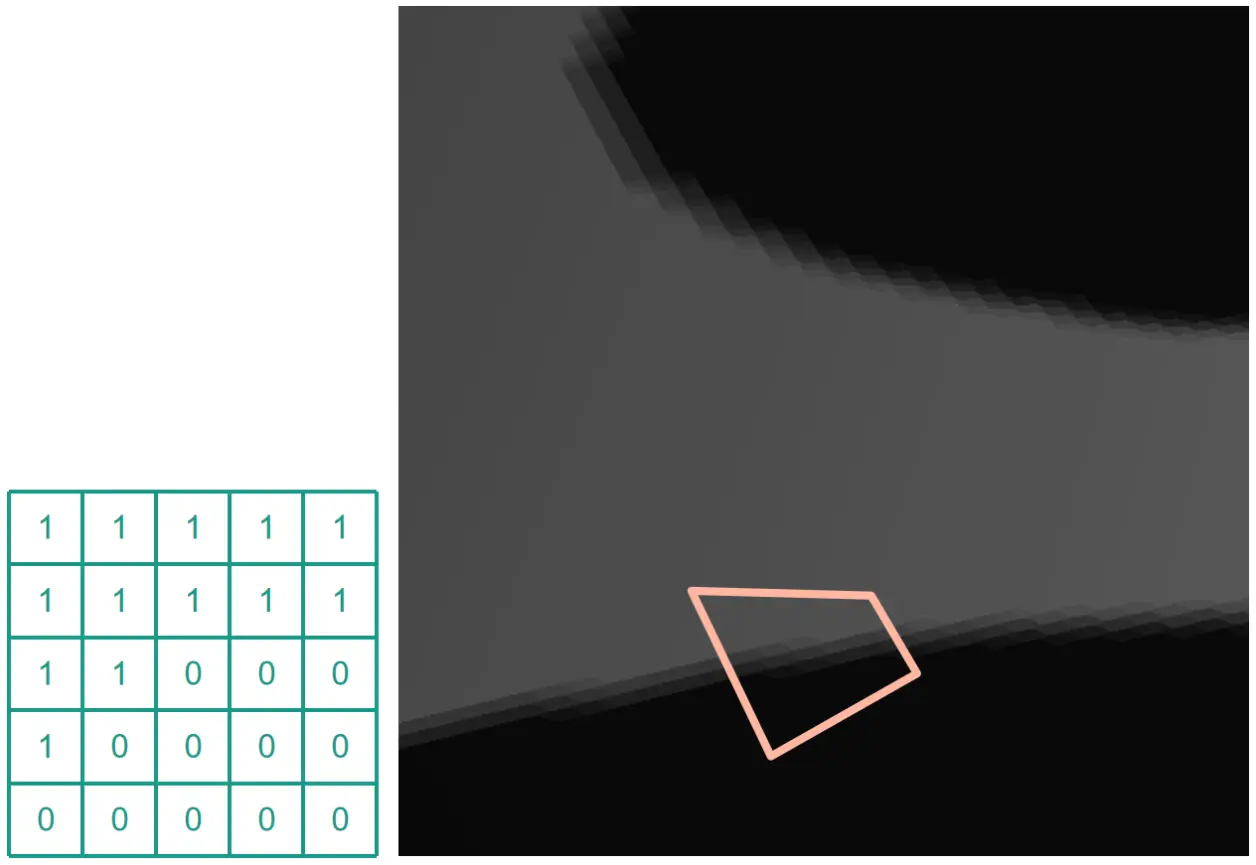
上面这得出的最终 $Visibility = 13 / 25 = 0.52$

采样窗口越大，抗锯齿效果就约好，但是当采样范围变大时，采样的次数成平方次膨胀，开销就会很大，达不到实时渲染的要求，因此我们可以在采样范围内，随机抽取一定个数（NUM_SAMPLES）的采样点进行采样，下面是一些常用的分布采样函数。

  • 均匀圆盘分布采样（Uniform-Disk Sample）：圆范围内随机取一系列坐标作为采样点；看上去比较杂乱无章，采样效果的 noise 比较严重。

  • 泊松圆盘分布采样（Poisson-Disk Sample）：圆范围内随机取一系列坐标作为采样点，但是这些坐标还需要满足一定约束，即坐标与坐标之间至少有一定距离间隔。

#define NUM_SAMPLES 20
vec2 poissonDisk[NUM_SAMPLES];

// 泊松圆盘分布
void poissonDiskSamples( const in vec2 randomSeed ) {

  float ANGLE_STEP = PI2 * float( NUM_RINGS ) / float( NUM_SAMPLES );
  float INV_NUM_SAMPLES = 1.0 / float( NUM_SAMPLES );

  float angle = rand_2to1( randomSeed ) * PI2;
  float radius = INV_NUM_SAMPLES;
  float radiusStep = radius;

  for( int i = 0; i < NUM_SAMPLES; i ++ ) {
    poissonDisk[i] = vec2( cos( angle ), sin( angle ) ) * pow( radius, 0.75 );
    radius += radiusStep;
    angle += ANGLE_STEP;
  }
}
// 均匀圆盘分布
void uniformDiskSamples( const in vec2 randomSeed ) {

  float randNum = rand_2to1(randomSeed);
  float sampleX = rand_1to1( randNum ) ;
  float sampleY = rand_1to1( sampleX ) ;

  float angle = sampleX * PI2;
  float radius = sqrt(sampleY);

  for( int i = 0; i < NUM_SAMPLES; i ++ ) {
    poissonDisk[i] = vec2( radius * cos(angle) , radius * sin(angle)  );

    sampleX = rand_1to1( sampleY ) ;
    sampleY = rand_1to1( sampleX ) ;

    angle = sampleX * PI2;
    radius = sqrt(sampleY);
  }
}

其中， rand_2to1, rand_1to1 1 是利用 $sin$ 函数特效实现的伪随机函数

// 伪随机函数
highp float rand_1to1(highp float x ) { 
  // -1 -1
  return fract(sin(x)*10000.0);
}

highp float rand_2to1(vec2 uv ) { 
  // 0 - 1
  const highp float a = 12.9898, b = 78.233, c = 43758.5453;
  highp float dt = dot( uv.xy, vec2( a,b ) ), sn = mod( dt, PI );
  return fract(sin(sn) * c);
}

PCF 算法过程：

  • 计算 Visibility 时，原本对 Shadow Map 的一次坐标采样，换成对周围一定范围内若干个坐标进行采样
  • 各个采样后的结果跟之前实际深度 $z^{'}$ 做比较，最后去平均值作为 Visibility
float PCF(sampler2D shadowMap, vec4 coords, float filterSize) {
  const float bias = 0.005;
  float sum = 0.0;
  // 初始化泊松分布
  poissonDiskSamples(coords.xy);
  // 采样
 
  for(int i = 0;i< NUM_SAMPLES;++i){
    float depthInShadowmap = unpack(texture2D(shadowMap, 
        coords.xy + poissonDisk[i] * filterSize).rgba);
    sum += ((depthInShadowmap + bias) < coords.z ? 0.0 : 1.0);
  }
  // 返还平均采样结果
  return sum/float(NUM_SAMPLES);
}

void main(void) {

  float visibility = 1.0;
  vec3 shadowCoordNDC = 
    (vPositionFromLight.xyz / vPositionFromLight.w + 1.0) / 2.0;

  // fiterSize 参数会影响实际采样区域的范围
  visibility = PCF(uShadowMap, vec4(shadowCoordNDC, 1.0), 0.001);

  vec3 phongColor = blinnPhong();

  gl_FragColor = vec4(phongColor * visibility, 1.0);
}

效果如下图所示，当 fiterSize 很小时，抗锯齿效果不明显（fiterSize = 0.0001），而当 fiterSize 逐渐增大时，阴影的边缘渐变效果越来越明显（ Shadow Map 的大小为 2048 * 2048）

当 Shadow Map 尺寸为 256 * 256 时，效果如下图：

PCF 通过增加采样区域范围，来做抗锯齿，当过滤范围变大时，逐渐有了软阴影的效果，因此，我们可以使用 PCF 的原理，来实现软阴影。

软阴影

较大的光源面在被物体遮挡时，阴影接收物上会有一部分区域被遮蔽了一部分光线，从而产生半影（Penumbra）。

PCSS (Percentage closer soft shadows)

之前介绍的 PCF 里，我们通过改变采样窗口，可以调整阴影整体的软硬程度，因此可以用这个方法来实现软阴影，不过我们注意到，投影面到遮挡物距离，会影响阴影的软化程度

钢笔尖的阴影距离钢笔近，产生的阴影很硬，轮廓很分明，笔身距离钢笔远，产生的阴影就很软，阴影边缘不清晰

因此，当我们对 PCF 进行一些改进，自动根据边缘半影的大小来计算过滤半径，就能很好的实现软阴影的效果，这就是 PCSS 的核心原理。

Penumbra Size（半影的大小）

根据半影的产生原因我们可以得出下面这个图

半影的大小取决于光源的大小（$W_{Light}$）以及距离遮挡物（Blocker）的距离（$d_{Receiver}$）

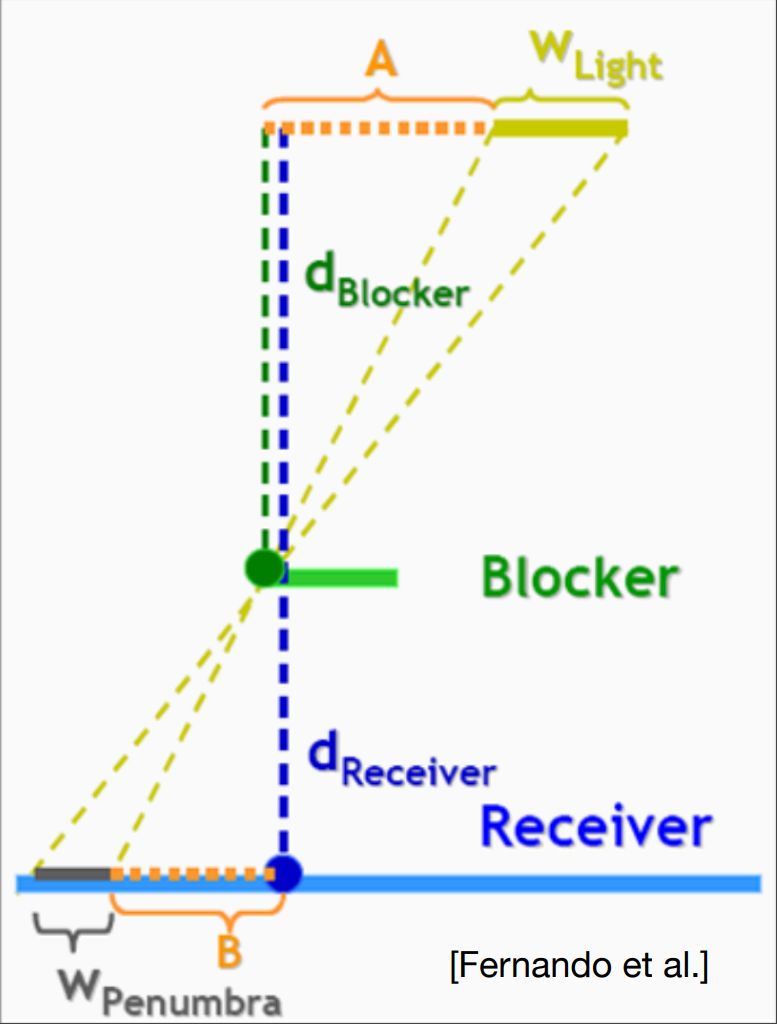
$$
w_{Penumbra} = \frac{(d_{Receiver} - d_{Blocker})* w_{light}}{d_{Blocker}}
$$

$w_{Penumbra}$ : 半影的长度
$d_{Receiver}$ : 阴影接收区域到光源距离
$d_{Blocker}$ : 遮挡物到到光源距离
$w_{light}$ : 光源的大小
$w_{Penumbra}$ 半影的长度可以看成是软阴影的范围

因此 PCSS 算法分为下面几个过程：

  • Blocker Search：计算得出 $d_{Blocker}$
  • 计算得出半影大小
  • 根据半影大小做 PCF
  1. 一般来说，Blocker Search 的时候不会只找单个像素点来获取 $d_{Blocker}$，会在像素周围一定范围内找遮挡，然后将所有是遮挡区域的深度求和再取平均值
  2. 对应大面积的灯光，理论上是不会产生硬阴影，因此一般会使用灯光的中心点作为点光源，生成 Shadow Map
#define NUM_SAMPLES 20
#define BLOCKER_SEARCH_NUM_SAMPLES NUM_SAMPLES

// 在附近 40 * 40 的范围内抽取 100 个像素点计算遮挡物平均深度
float findBlocker( sampler2D shadowMap,  vec2 uv, float zReceiver ) {
  // 初始化泊松分布
  poissonDiskSamples(coords.xy);

  const int radius = 40;
  const vec2 texelSize = vec2(1.0/2048.0, 1.0/2048.0);
  float cnt = 0.0, depthSum = 0.0;
  float is_block = 0;
  float EPS = 0.002;
  for(int ns = 0; ns < BLOCKER_SEARCH_NUM_SAMPLES; ++ns)
  {
      vec2 sampleCoord = (vec2(radius) * poissonDisk[ns]) * texelSize + uv;
      float depthOnShadowMap = unpack(texture2D(shadowMap, sampleCoord));
      is_block = step(depthOnShadowMap, zReceiver - EPS)
      cnt += is_block;
      depthSum += is_block * depthOnShadowMap;
  }
  if(cnt < 0.1)
  {
    return zReceiver;
  }
  return depthSum / cnt;
}

float PCF(sampler2D shadowMap, vec4 shadowCoord, float radius) {
  const vec2 texelSize = vec2(1.0/2048.0, 1.0/2048.0);
  float visibility = 0.0, cnt = 0.0;
  for(int ns = 0;ns < PCF_NUM_SAMPLES;++ns)
  {
    vec2 sampleCoord = (vec2(radius) * poissonDisk[ns]) * texelSize 
        + shadowCoord.xy;

    float cloestDepth = unpack(texture2D(shadowMap, sampleCoord));
    visibility += ((shadowCoord.z - 0.001) > cloestDepth ? 0.0 : 1.0);
    cnt += 1.0;
  }
  return visibility/cnt;
}

float PCSS(sampler2D shadowMap, vec4 shadowCoord){

  // STEP 1: avgblocker depth
  float avgBlockerDepth = findBlocker(shadowMap, shadowCoord.xy, shadowCoord.z);

  // STEP 2: penumbra size
  const float lightWidth = 50.0;
  float penumbraSize = max(shadowCoord.z - avgBlockerDepth, 0.0) / 
    avgBlockerDepth * lightWidth;

  // STEP 3: filtering
  return PCF(shadowMap, shadowCoord, penumbraSize);
  //return 1.0;

}

结果如下图所示：

缺点

从实现步骤上，PCSS 有两个地方非常耗时，需要多次采样图片。

  • Blocker Search：计算得出 $d_{Blocker}$
  • 根据半影大小做 PCF

VSSM 方差软阴影映射算法 (Variance soft shadow mapping)

加速 PCF 计算方案

从上面的介绍可以得知，PCSS 有两个耗时的地方，我们首先来看 PCF 这个耗时点。PCF 的本质是在特定区域内，对每一个像素都采样深度贴图，将采样的到的值跟当前实际深度对比，小于则返回 0 大于返回 1（例如 10 * 10 的区域内，有 40 个小于的，则最终返回 40 / 100），这个等价于找到当前区域内，给定一个深度 $D_{scene}$，当前点在 Shadow Map 上的深度为 $D_{SM}$，求 $D_{SM} > D_{scene}$ 的概率 $P(D_{SM} > D_{scene})$

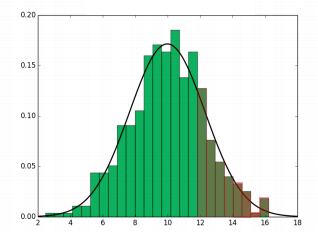
上图是把当前区域所有的像素值在 Shadow Map 上的深度做的直方图，横坐标表示当前深度值，绿色的区域表示当前深度的像素个数，个数越多，柱状图越高，深色区域表示深度大于等于 12 的像素个数

VSSM 的思想是，将某个区域的深度值近似的看成是正态分布，那对于一个正态分布我们只需要知道两个变量均值（期望）$E$，方差 $Var$，平均值很好求，方差可以用下面的公式求得：

$$
Var(X) = E(X2)-E2(X)
$$

  1. $E(X)$: 深度图某个区域内像素的平均值
  2. $E^2(x)$：另外一张深度图，记录的是深度值的平方，求给定区域像素的平均值
  3. 怎么快速计算指定区域内像素的均值，后面会讲

当我们有了期望跟方差后，就能得出一个正态分布的函数图，那我们之前要求的百分比 $P(D_{SM} > D_{scene})$，就是下图中 1 - 阴影的面积：

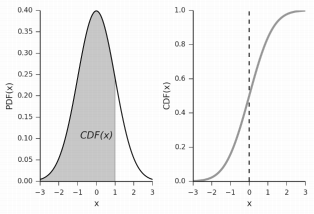
VSSM 为了求解上面的百分比，使用切比雪夫不等式来求解，切比雪夫不需要知道具体的分布函数的，不一定需要是正态分布。

$$
\begin{align*}
P(x > t) &\leq \frac{\sigma ^2}{\sigma ^2 + (t - \mu)^2} \
P(x > t) &\approx \frac{\sigma ^2}{\sigma ^2 + (t - \mu)^2}
\end{align*}
$$

$x$ ：分布函数里的变量 $x$
$t$ ：某个指定的值
$\sigma$ : 标准差
$\mu$ : 均值

限制：

  • $t$ 必须在均值右边，不然不准（实时渲染里，还是这么使用）

加速 Block Search 计算方案

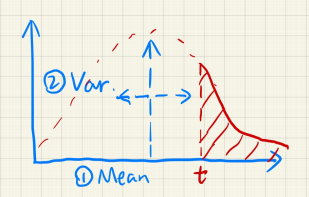
现在回到第一步 Blocker Search 的计算上，我们有如下区域深度信息，当前像素光照位置的的真实深度是 7 则所有深度小于 7 的像素就是要找的 Blocker，即下图中的蓝色区域。

对于这个区域会有下面这个等式成立：$Z_{occ}$ 就是我们要求的 Blocker 的平均深度

$$
\frac{N_{1}}{N}Z_{unocc} + \frac{N_{2}}{N}Z_{occ} = Z_{avg}
$$

t : 当前深度
$Z_{occ}$：所有深度小于 $t$ 的深度平均值
$Z_{unocc}$: 所有深度大于等于 $t$ 的深度的平均值
$N$ : 当前区域像素点个数
$N_1$：深度大于等于 $t$ 的像素个数
$N_2$：深度小于 $t$ 的像素个数
$Z_{avg}$：当前区域所有像素的深度的平均值

沿用之前 PCF 中的假设

$$\begin{align*}
\frac{N_{1}}{N} &= P(x>t) \
\frac{N_{2}}{N} &= 1 - P(x>t)
\end{align*}
$$

剩下 $Z_{unocc}$ 不知道值，这个时候，VSSM 做了个大胆的假设，假设投影接收区域是个平面，直接使用估计值，令 $Z_{unocc} = t$，就能立刻计算出 $Z_{occ}$

区域均值

综上所述，不管 PCF，还是 Blocker Search 加速方法，都需要计算某个区域内的像素的均值，均值的求解方法：

Mipmap

最简单的方法就是使用 Mipmap 来快速获取贴图上某个区域的均值，但是 Mipmap 获取的值也是通过插值获取的近似值（三线性插值）

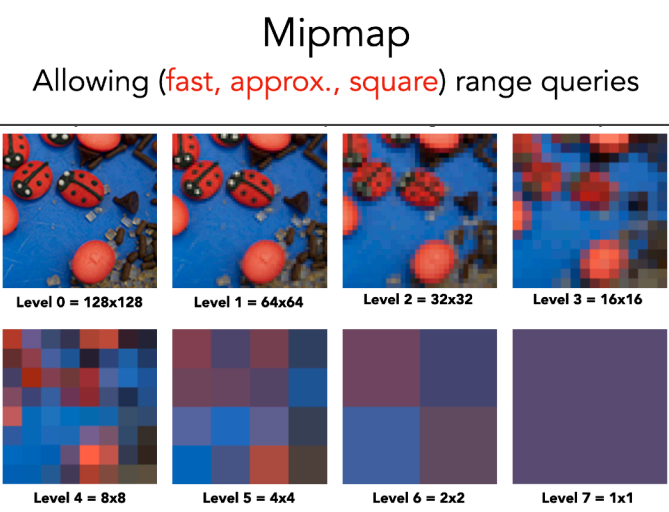
SAT（Summed-Area Table）二维面积前缀和

先介绍一维的 SAT，如下图 SAT 存储的是当前位置之前所有的数的总和

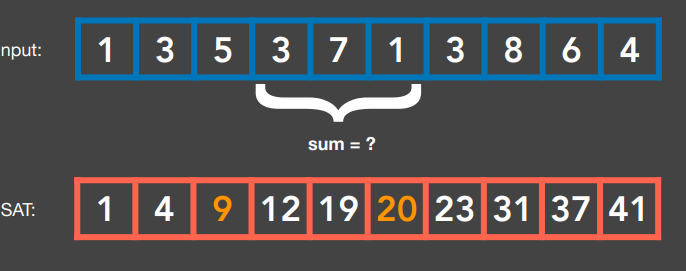
当我们要求括号区域的值的平均值时，只需要找到区间前一个位置的和跟区间最后一个位置的和，做减法即可快速得到当前区间内的像素的和。

扩展到二维：

  • 首先跟一维 SAT 一样，逐行计算每行的 SAT
  • 然后再逐列遍历，计算每行的 SAT

然后我们要计算某个区域的平均值时，如下图蓝色框框是我们要计算的区域

$$
S = S1 - S2 - S3 + S4
$$

VSSM 效果

VSSM 缺点

  • 假设区域内像素分布为正态分布，如果采样区域不符合正态分布，阴影效果就不正确

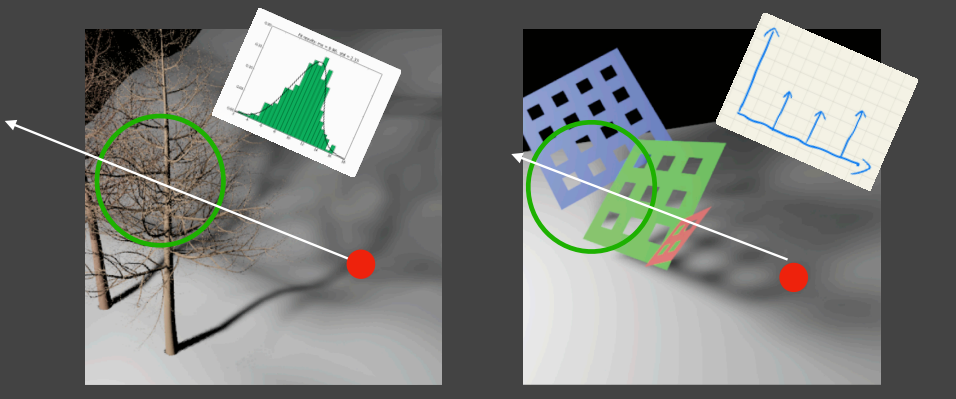
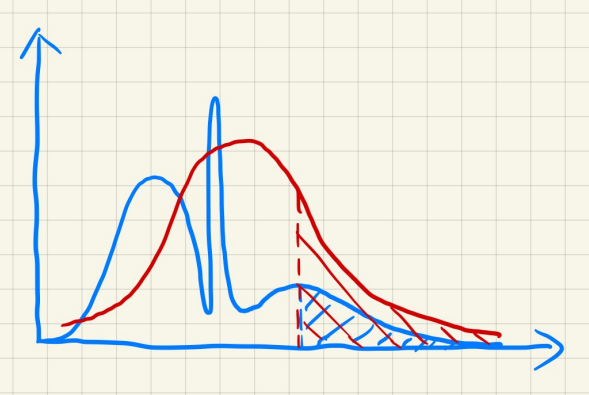
右图的阴影分布呈现比较规则的分布，深度值会几种在三个面片附近，如下图所示，会有三个波峰

当估计值偏高时，如下图，则计算得出的 Visibility 的值偏大（1 为可见，0 为全黑），就会导致漏光，车底盘出现了漏光现象（Light Leaking）。

当估计值偏小时，得出的阴影会更黑，人眼不容易观察出来。

  • 之前计算 Blocker Search 的时候， VSSM 大胆假设了投影接收物体是一个平面 $Z_{unocc} = t$，但实际上有些情况，投影接收物体不一定是个平面

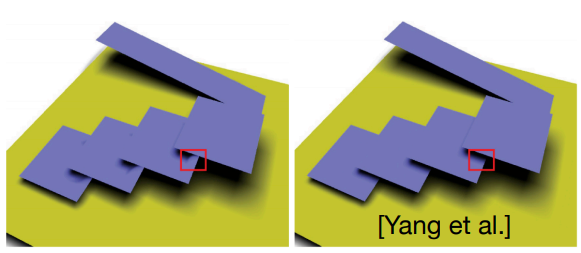
左图中的几个面片是倾斜的，是的阴影接收面是一个斜面。

  • 切比雪夫不等式应用上问题：大于均值区域不等式才成立

MSM（Moment Shadow Mapping）

MSM 主要是解决在 PCF 阶段，描述分布不准导致漏光的问题，VSSM用深度的均值 $\mu$
和方差 $\sigma$ 来逼近可见性的累积分布函数，本质上是利用深度值分布的一阶原始矩和二阶中心距，MSM 采用更高阶的矩来进行估计（前四阶矩），不考虑精度的情况下，分别用 Shadow Map 的四个通道存储 $z$，$z2$，$z3$，$z^4$

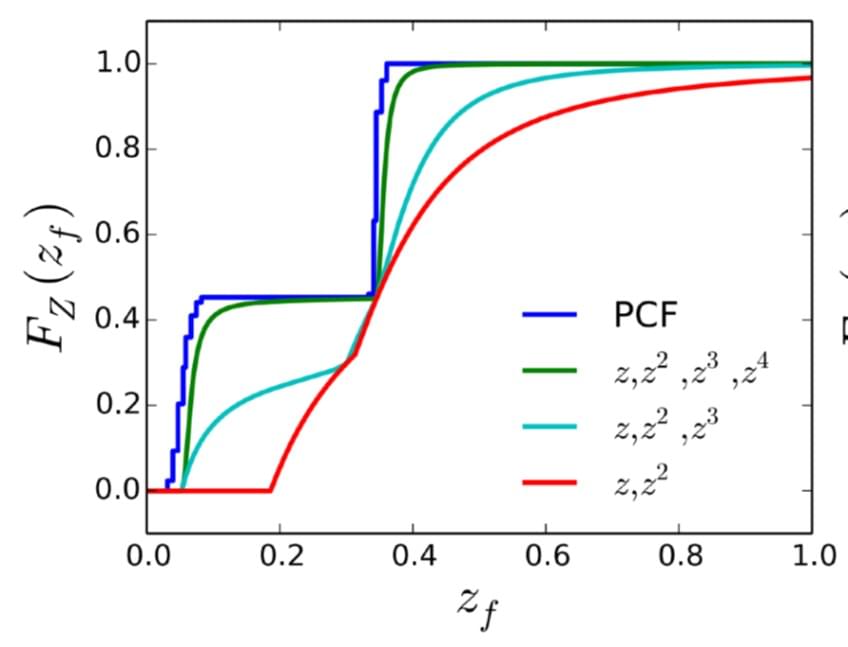
可以类比成泰勒展开，保留的次方越高，拟合效果越接近。

下面是 VSM（PCF 的优化版本， VSSM 是 PCSS 的优化版本）对比效果

Distance Field Soft Shadows（距离场软阴影）

之前在介绍文本的时候，介绍过 SDF 的文本，距离场也可以用在实时阴影中，假设我们已经知道场景中任何一个点到最近物体的距离场后，可以利用距离场近似计算软阴影，软阴影的产生其实是光源一部分光线被遮挡了，如下图，则半影的大小跟图中的 $\theta$ 角度（当前渲染点到光源中心方向上与最近的遮挡物所形成的最小安全角）成正比。

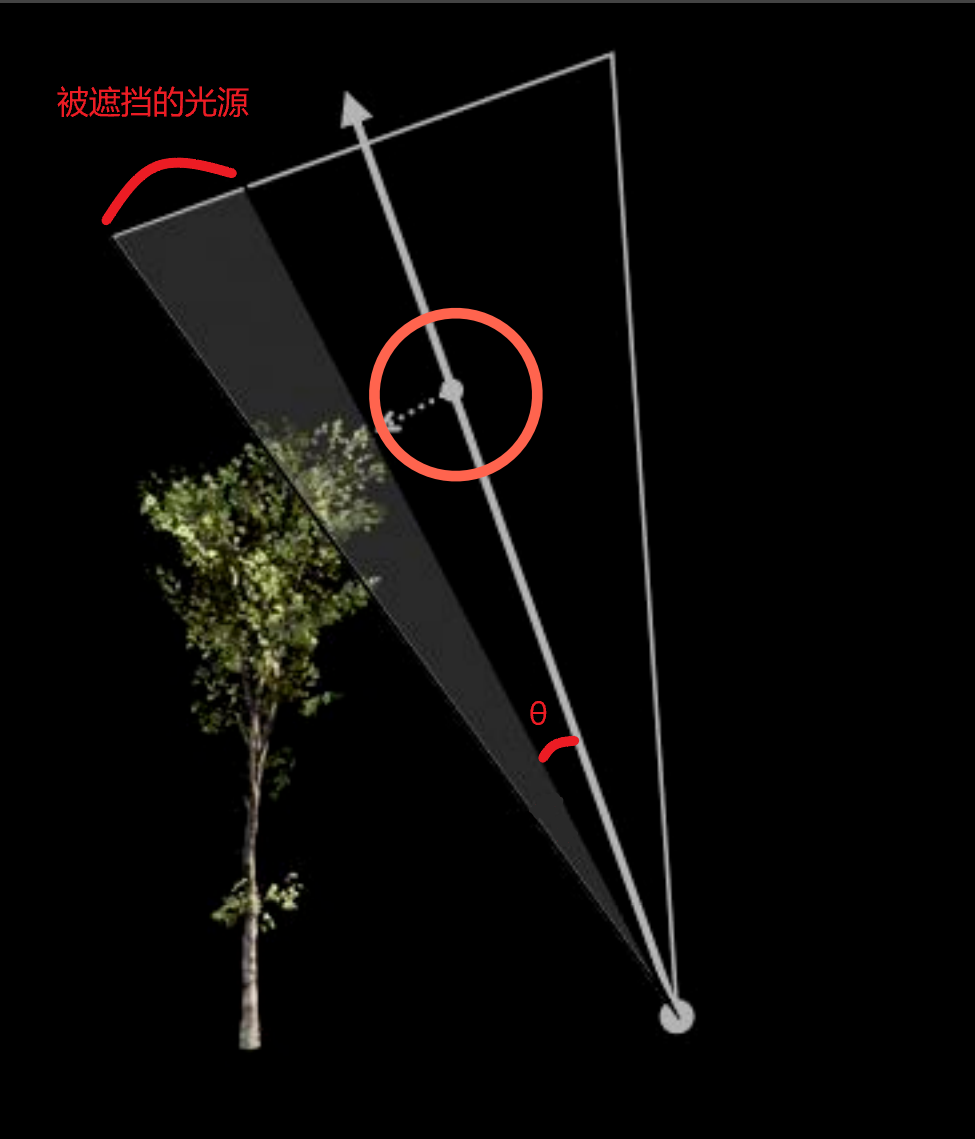
SDF 将阴影求解转换求解安全角度

当我们有了整个场景的 SDF 数据后，我们首先从渲染点 $P0$ 出发，找到该点最近遮挡物的距离（红色圆圈），然后继续沿着该方向找到下一个点 $P1$，继续找到 $P1$ 点到最近遮挡物的距离，以此类推，从而找出该方向上最小的距离。

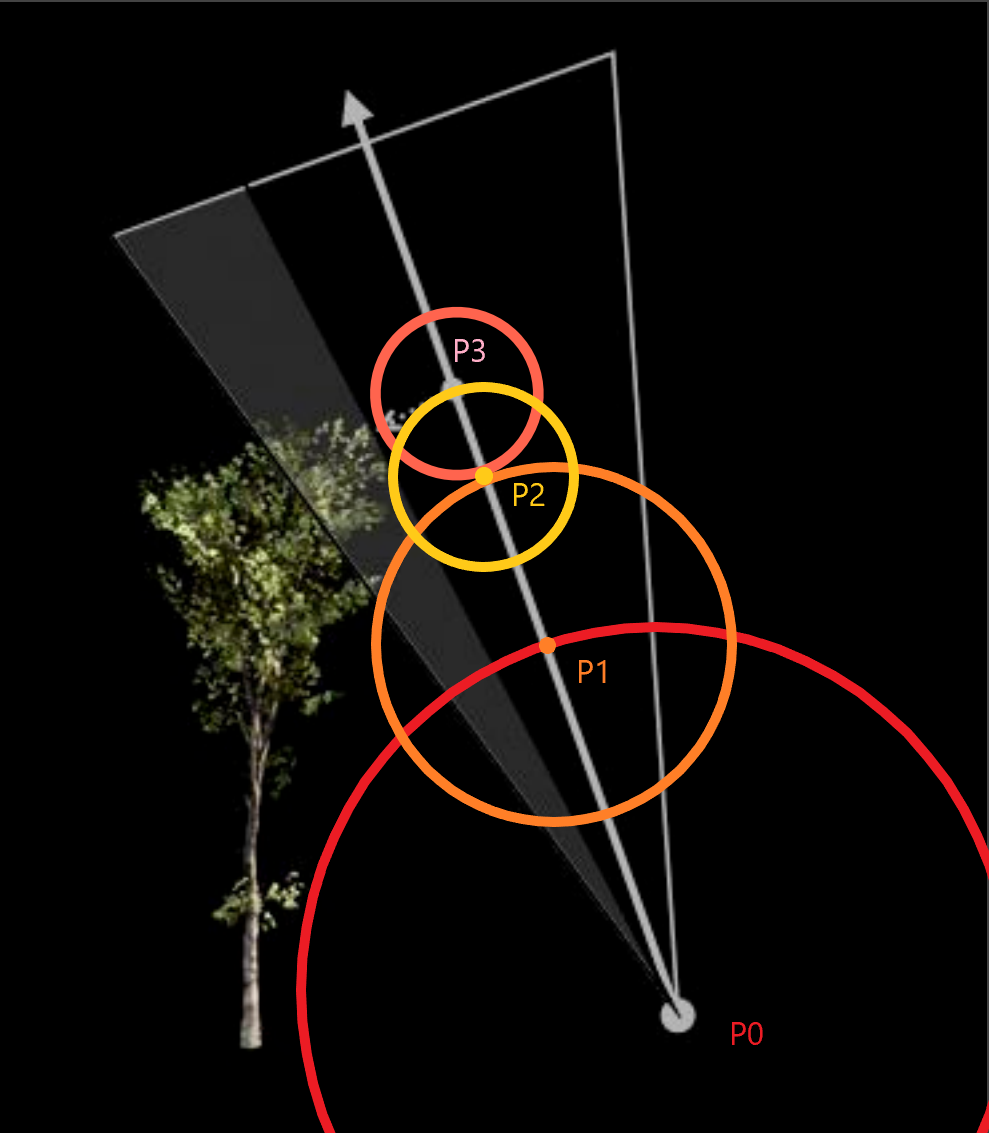
然后将所有圆跟起点 $P0$ 做切线得出下面这个图：

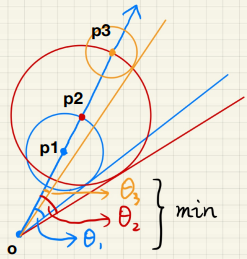
SDF 只能告诉我们当前点最近的遮挡物距离，但是不知道遮挡物的方向，因此这里对圆做切线，将切线处当成遮挡物位置(切线处角度最大)

因此 $\theta$ 求解公式如下：

$$
\theta = arcsin(\frac{SDF(p)}{|p-o|})
$$

但是在实际中，会用下面这个式子来做近似

$$
min \left { \frac{k \cdot SDF(p)}{|p-o|}, 1.0
\right }
$$

// ro: o 点
// rd: o 点到光源中心点方向向量
float softshadow( in vec3 ro, in vec3 rd, float mint, float maxt, float k )
{
    float res = 1.0;
    for( float t = mint; t < maxt; )
    {
        float h = map(ro + rd * t);
        if( h < 0.001 )
            return 0.0;

        res = min( res, k * h / t );
        t += h;
    }
    return res;
}

优点

  • 计算速度快（假设 SDF 已经离线生成的情况下，比传统的 Shadow Mapping 技术快很多
  • 阴影质量很高，完美解决 Shadow Ance（自遮挡），Peter Panning（阴影浮空）等问题

缺点

  • SDF 需要预计算，因此场景中的物体需要是静态的
  • SDF 需要大量的存储空间（一般采用三维数组来存储空间中各个网格的 SDF 值）

参考

1.高质量实时渲染（一）——实时阴影（1）

2.高质量实时渲染（二）——实时阴影（2）

3.高质量实时渲染：实时软阴影

4.实时阴影技术（Real-time Shadows）

5.GAMES202-高质量实时渲染 —— Lecture3 Real-time Shadows

6.联级阴影贴图CSM(Cascaded shadow map)原理与实现

7.联阴影映射

8.利用 Shader 生成伪随机数

9.图形学基础 - 阴影 - ShadowMap及其延伸

10.Variance Soft Shadow Mapping (实时软阴影)

11.入门Distance Field Soft Shadows