FSR 技术原理

发表于 2023-10-27 分类于 Graphics 阅读次数：本文字数： 11k 阅读时长 ≈ 10 分钟

FidelityFX-FSR 1.0（FidelityFX Super Resolution）是 AMD 开源的超分算法，这个算法不像 NVIDIA 的大力水手（DLSS）使用了机器学习算法，总体来说是对边缘进行锐化后的图像放大思想，效果上没有非常逆天，但是扩展性高，适用于各种显卡平台，且开销低 ¹（这篇文章里说用到 17 = 12 + 5 次采样）

上采样跟下采样

上采样：原先有一张小尺寸的纹理，然后我们将这个纹理放大到大尺寸中，然后使用采样方法（例如双线线性插值）进行填充。
下采样：原先有一张大尺寸的纹理，然后将这个纹理缩小到一个小尺寸中。

FSR 流程跟简介

AMD 官方文档 ² 给出了几个缩放比例，以及对应分辨率超分后得到的输出分辨率，缩放比例越多，性能提升越多，但同时画质会有所降低，如下图所示：

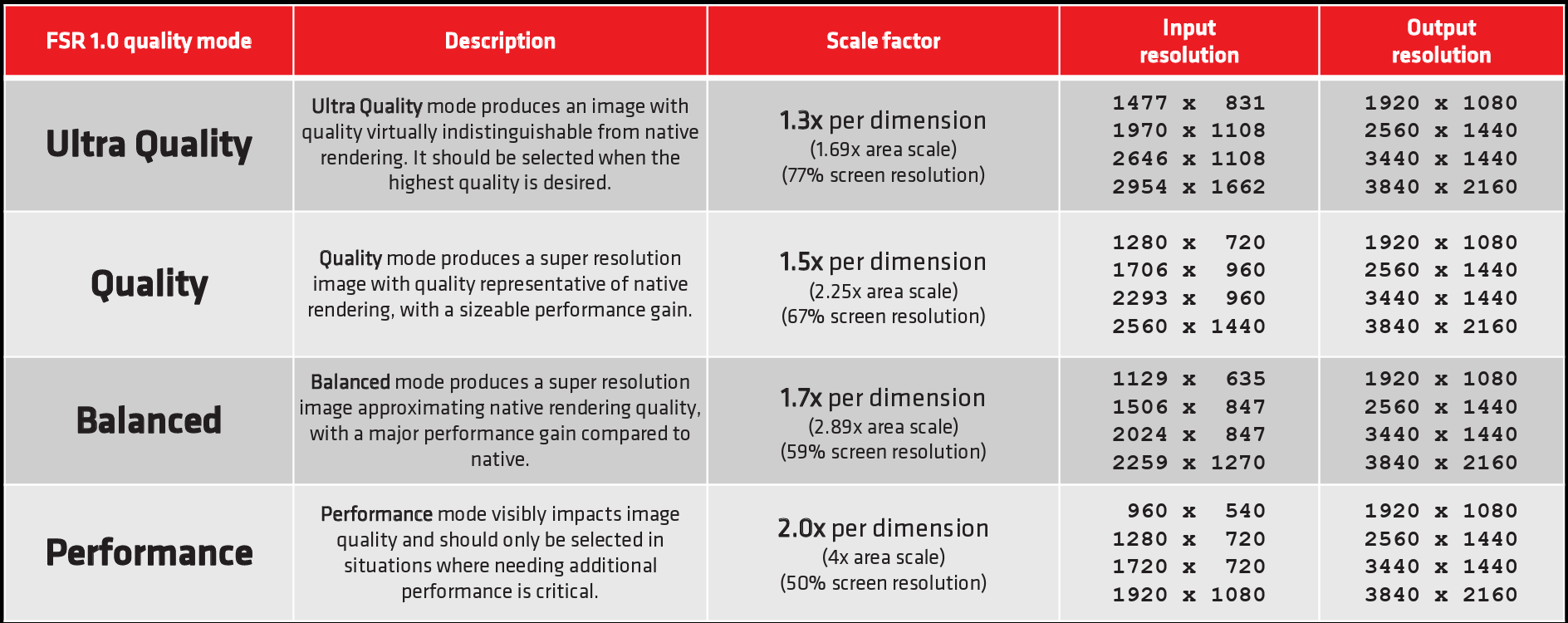
FSR 管线

AMD 官方文档中给出了 FSR 使用前提：

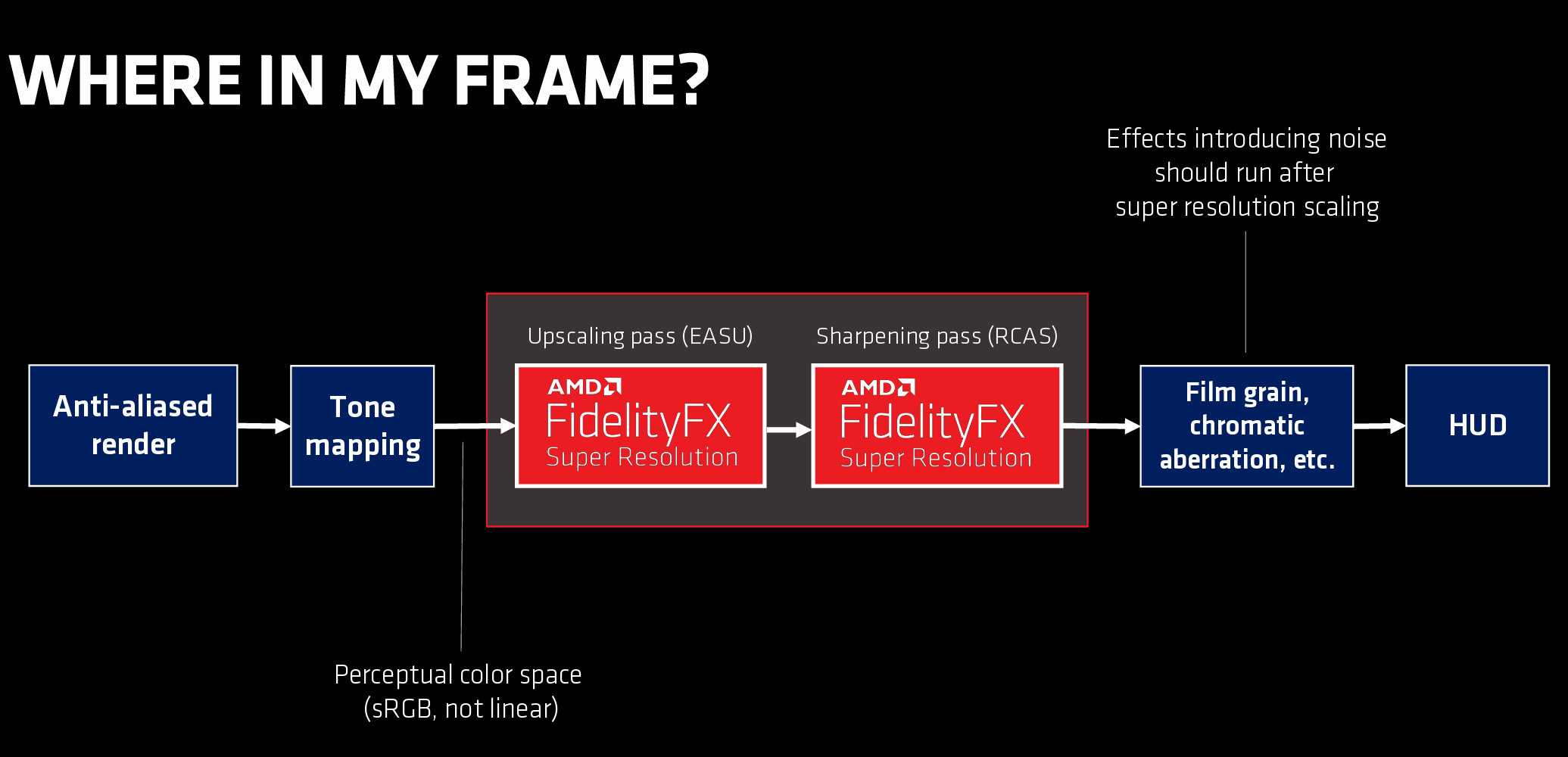
进行 FSR 之前，图像必须已经是做过抗锯齿后的，因此 FSR 必须在 TAA，MSAA， Tone maping 后面。
图像中的像素值必须是标准化的，像素值范围在 [0-1]
渲染得到的图像必须要要使用负的 Mip 修正来增加图像细节
图像没有噪声

下图是官方给的 FSR 的管线图：

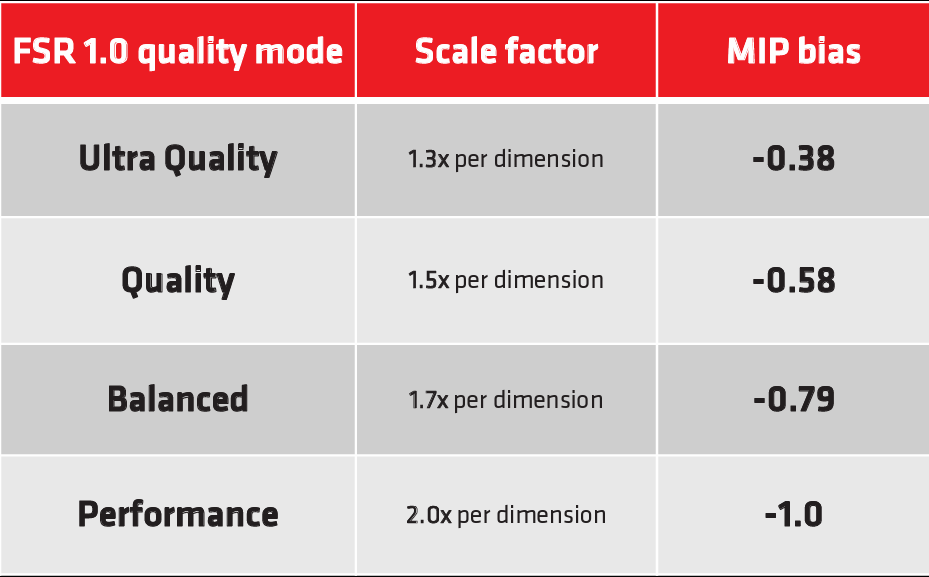
超分前，渲染分辨率是比较小的，因此渲染时会使用比较高级别的 mipmap 贴图，因此为了提高图像细节，可以根据超分比例增加 mipmap 偏移），下面是对应缩放比例下 MIP bias 偏移值对照表。
$MIP bias = -\log2(ScaleFactor)$

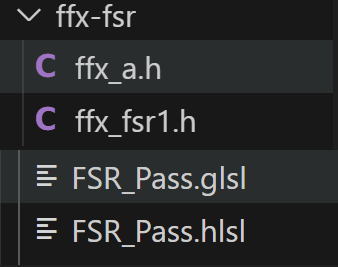
FSR 代码组成

FSR 代码很简单，主要包含一个 Shader 文件以及两个 C++/Shader 用到的 .h 头文件

DX12 下的实现

可以下载 FidelityFX-FSR 源码，按照文档安装环境 CMake 后，执行对应的批处理，生成对应的 DX12 或者 Vulkan（需要安装 Vulkan DK）工程，然后点击对应的工程编译生成示例工程，官方工程里是在 TAA，Tone mapping 之后增加一个 FSR 流程，然后使用 Compute Shader 来做超采。

// FidelityFX-FSR\sample\src\DX12\SampleRenderer.cpp
void SampleRenderer::OnRender(int displayWidth, int displayHeight, 
    State *pState, SwapChain *pSwapChain)
{
    // TAA
    // Tone mapping
    m_FSR.Upscale(pCmdLst2, displayWidth, displayHeight, pState, 
        &m_ConstantBufferRing, hdr);
}

m_FSR 创建的时候会加载 FSR_Pass.hlsl 并编译 Shader，这里会传入 Shader 编译用到的宏定义，以及指定线程组中的线程数量。

// 使用时记得引用 FSR 给的头文件，这里包含一些数据格式
// 以及用来计算 uniform 常量的函数 FsrEasuCon
#include "ffx_a.h"
#include "ffx_fsr1.h"

// FidelityFX-FSR\sample\src\DX12\FSR_Filter.cpp
void FSR_Filter::OnCreate()
{
    defines["SAMPLE_RCAS"] = "0";
    defines["SAMPLE_EASU"] = "1";

    m_easu.OnCreate(pDevice, pResourceViewHeaps, "FSR_Pass.hlsl", "mainCS", 1, 1, 
        64, 1, 1, &defines, 1, &sd);

    // NVIDA 中调度的基本单位 warp 大小是 32 个线程
    // AMD   中调度的基本单位 warefront 大小是 64 个线程
    // 因此这里采用了 64 的倍数
    // cs 代码中每个线程组创建 64 * 1 * 1 线程

    // m_easu.OnCreate 函数调用会定义如下三个宏，在 FSR_Pass.hlsl 中会用到
    // defines["WIDTH" ] = std::to_string(params.dwWidth);
    // defines["HEIGHT"] = std::to_string(params.dwHeight);
    // defines["DEPTH" ] = std::to_string(params.dwDepth);
    
    defines["SAMPLE_EASU"] = "0";
    defines["SAMPLE_RCAS"] = "1";
    // cs 代码中每个线程组创建 64 * 1 * 1 线程
    m_rcas.OnCreate(pDevice, pResourceViewHeaps, "FSR_Pass.hlsl", "mainCS", 1, 1, 
        64, 1, 1, &defines, 1, &sd);
}

每帧渲染时 FSR 更新分为三个步骤：

FsrEasuCon：计算 FSR 用到的常数 uniform，用于计算像素点对应超采前像素位置信息
EASU：调用 easu Compute Shader 进行上采样
RCAS：调用 rcas Compute Shader 进行锐化操作

struct FSRConstants
{
    XMUINT4 Const0;
    XMUINT4 Const1;
    XMUINT4 Const2;
    XMUINT4 Const3;
    XMUINT4 Sample;
};

void FSR_Filter::Upscale(ID3D12GraphicsCommandList* pCommandList, int displayWidth, 
    int displayHeight, State* pState, DynamicBufferRing* pConstantBufferRing, 
    bool hdr)
{
    /// Step 1:
    FsrEasuCon(reinterpret_cast<AU1*>(&consts.Const0), 
        reinterpret_cast<AU1*>(&consts.Const1), 
        reinterpret_cast<AU1*>(&consts.Const2), 
        reinterpret_cast<AU1*>(&consts.Const3), 
        static_cast<AF1>(pState->renderWidth), 
        static_cast<AF1>(pState->renderHeight), 
        static_cast<AF1>(pState->renderWidth), 
        static_cast<AF1>(pState->renderHeight), 
        (AF1)displayWidth, (AF1)displayHeight);

    /// 将超采图像按照 16 * 16 大小分割成若干个线程组
    /// 超采后分辨率 1920 * 1080 会对应创建 120 * 68 个 compute shader 线程组
    static const int threadGroupWorkRegionDim = 16;
    int dispatchX = (displayWidth + (threadGroupWorkRegionDim - 1)) / 
        threadGroupWorkRegionDim;

    int dispatchY = (displayHeight + (threadGroupWorkRegionDim - 1)) / 
        threadGroupWorkRegionDim;

    /// Step 2:
    m_easu.Draw(pCommandList, cbHandle, &m_intermediaryUav, &m_inputTextureSrv, 
        dispatchX, dispatchY, 1);

    /// Step 3:
    m_rcas.Draw(pCommandList, cbHandle, &m_outputTextureUav, &m_intermediarySrv, 
        dispatchX, dispatchY, 1);
}

FSR 中对图片处理的切割如下图所示，将超分图像按照 16 * 16 切分成块，每个线程组处理一块，然后在 CS 中将 16 * 16 的块切分成 8 * 8 的小块，对应 8 * 8 个线程，每个线程处理 4 个像素，如下图紫色框所示：

// FidelityFX-FSR\sample\src\DX12\FSR_Pass.hlsl

// 每个线程组中对应的线程数量是：64 * 1 * 1 
[numthreads(WIDTH, HEIGHT, DEPTH)]
void mainCS(uint3 LocalThreadId : SV_GroupThreadID, uint3 WorkGroupId : SV_GroupID, 
    uint3 Dtid : SV_DispatchThreadID)
{
    // 根据线程组 WorkGroupId 我们可以知道当前处理的切片编号（例如上图右边 粉红色区域 (2, 1) ）
    // 根据线程 LocalThreadId 我们可以知道当前处理的是左上角 8 * 8 中的像素编号
    //  （例如上图 A 区域中的紫色像素  (3, 2) ）
    AU2 gxy = ARmp8x8(LocalThreadId.x) + AU2(WorkGroupId.x << 4u, WorkGroupId.y << 4u);

    /// A 区域
    CurrFilter(gxy);

    /// B 区域
    gxy.x += 8u;
    CurrFilter(gxy);

    /// C 区域
    gxy.y += 8u;
    CurrFilter(gxy);

    /// D 区域
    gxy.x -= 8u;
    CurrFilter(gxy);
}

void CurrFilter(AU2 pos)
{
#if SAMPLE_EASU
    AH3 c;
    FsrEasuH(c, pos, Const0, Const1, Const2, Const3);
    if( Sample.x == 1 )
        c *= c;
    imageStore(OutputTexture, ASU2(pos), AH4(c, 1));
#endif
#if SAMPLE_RCAS
    AH3 c;
    FsrRcasH(c.r, c.g, c.b, pos, Const0);
    if( Sample.x == 1 )
        c *= c;
    imageStore(OutputTexture, ASU2(pos), AH4(c, 1));
#endif
}

FSR 超分部分

FSR 超分部分包含两个部分，上采样（EASU）+ 锐化（RCAS），接下来对这几部分做详细分析。

EASU（Edge Adaptive Spatial Upsamping）

首先我们看下使用双线性插值来做图像放大的效果，下面是一张 128 * 128 的图片，我们将其放大 2 倍。

可以看到，图像出现了模糊，主要是因为边缘部分的像素出现了锯齿，因此在放大图像的过程中，需要对边缘部分进行特殊处理。

边缘跟非边缘的上采样

使用 EASU 进行上采样，对图像进行放大时，放大后的像素有两种情况

非边缘：如果是非边缘，则对于放大后的像素点 $P$，在原图对应像素点 $Q$，则 $Q$ 附近的像素灰度应该非常接近，此时只需要对 $Q$ 周围的像素进行加权平均即可：

$$
f(P) = \frac{\sum_i f(Q_i)\omega_i}{\sum_i \omega_i} \tag{1}
$$

$f(x)$: 采样像素 x 点的灰度值
$\omega_i$: 为权重（正数）

边缘：如果此时像素点 $P$ 为边缘时，如果按照公式 (1) 处理，则边缘就会变模糊，因此根据边缘锐化的思路，对边缘进行上采样为：

$$
f(P) = f(Q) + \lambda F(Q) \tag{2}
$$

$F(Q)$: 为高频滤波器，用来提取边缘信息
$\lambda$: 为缩放因子

例如：4 邻域的 拉普拉斯算子 就是一个常用的高频滤波器（图像边缘处的像素变化大，也就是高频数据）

使用算子后得到：

$$
F(Q)=|4f(Q_{x,y}) - f(Q_{x-1, y}) - f(Q_{x+1, y}) - f(Q_{x,y-1}) - f(Q_{x, y+1})| \tag{3}
$$

如果 $Q_{x,y}$ 周围像素的灰度值变化越小（低频，非边缘），则 $F(Q)$ 越小，灰度值变化越大（高频，边缘）则 $F(Q)$ 越大。其实本质上还是加权法，只是权重有负数（为了计算像素之间的差值）。

因此可以将边缘跟非边缘的计算方法统一成一个表达式：

$$
f(P) = \frac{\sum_i f(Q_i)H(Q_i)}{\sum_i H(Q_i)} \tag{4}
$$

$H(Q_i)$: 权重计算公式，而且应该满足当 Q 点为非边缘时，权重为正数，Q 点为边缘时，$H(Q_i)$ 中会包含负的权重，用来计算高频滤波器，因此接下来就是要找到满足这样条件的权重计算公式。

Lanczos2 函数

EASU 引入了 Lanczos 函数：

$$
L(x) = \frac{asin(\pi x)sin(\frac{\pi x}{a})}{\pi^2 x^2}, x \in [-a, a] \tag{5}
$$

当 $a = 2$ 时，通常将其成为 Lanczons2 函数， EASU 就是基于 Lanczos2 函数作为基础处理的，它的图像如下图所示。

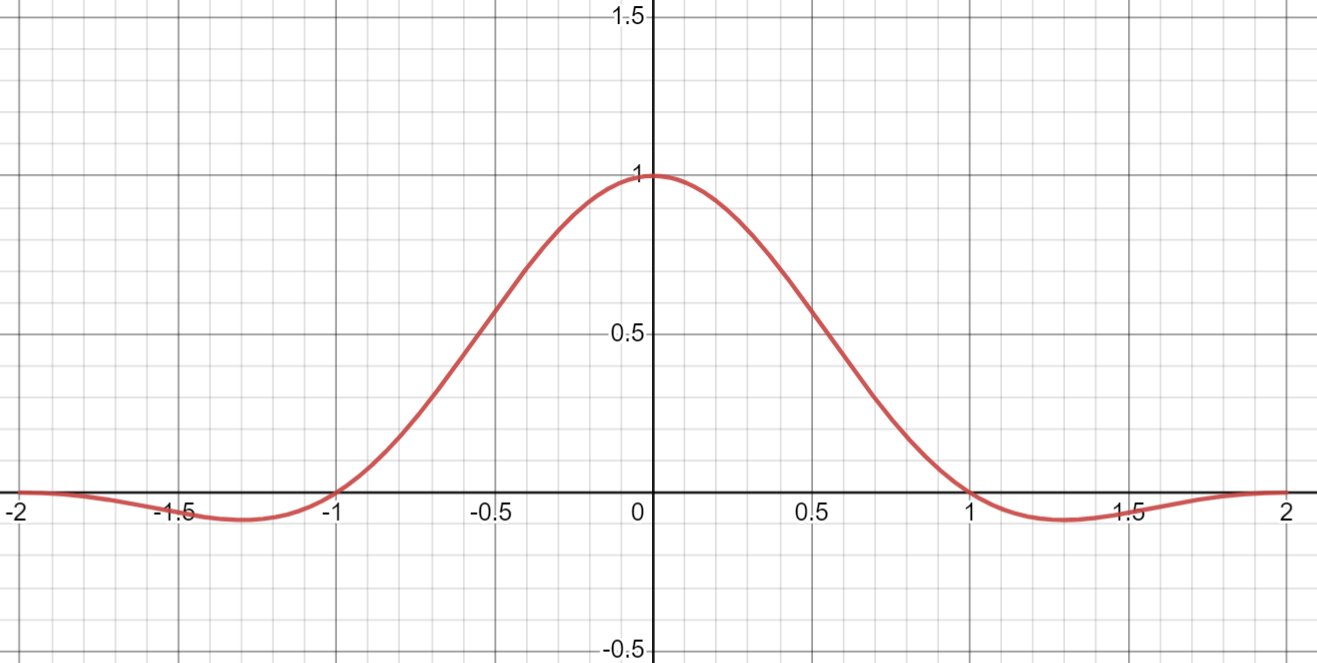
Lanczons2 函数的值在 $x\in [0,1]$ 时函数值大于 0，$x \in [1, 2]$ 部分，函数值小于 0。但是函数包含了三角函数，在 Shader 中效率不高，因此 EASU 用多项式来拟合公式 (5)。

$$
L(x) = \left[\frac{25}{16}\left( \frac{2}{5} x^2 - 1 \right)^2 - \left( \frac{25}{16} - 1 \right) \right](\omega x^2 - 1)^2 \tag{6}
$$

其中 $\omega$ 参数可以用来控制函数在 $x \in [1, 2]$ 部分的值，下面是 $w$ 从 0 变化到 0.5 过程中的函数图像

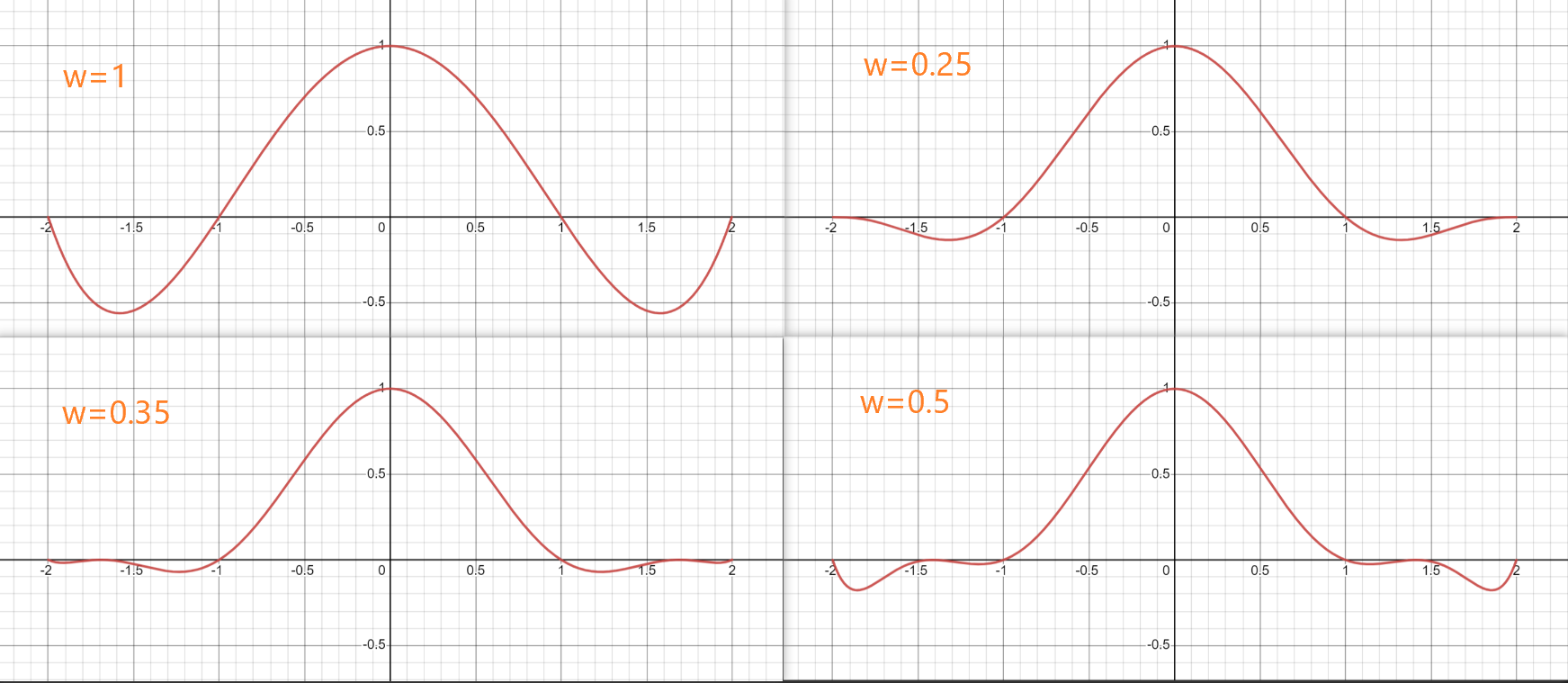
拖拽紫色的拖拽点，可以改变 $\omega$ 的值，点击右下角 desmos 可以跳转对应的公式编辑器。

边缘特征

图像中的边缘，一般有如下几种情况：

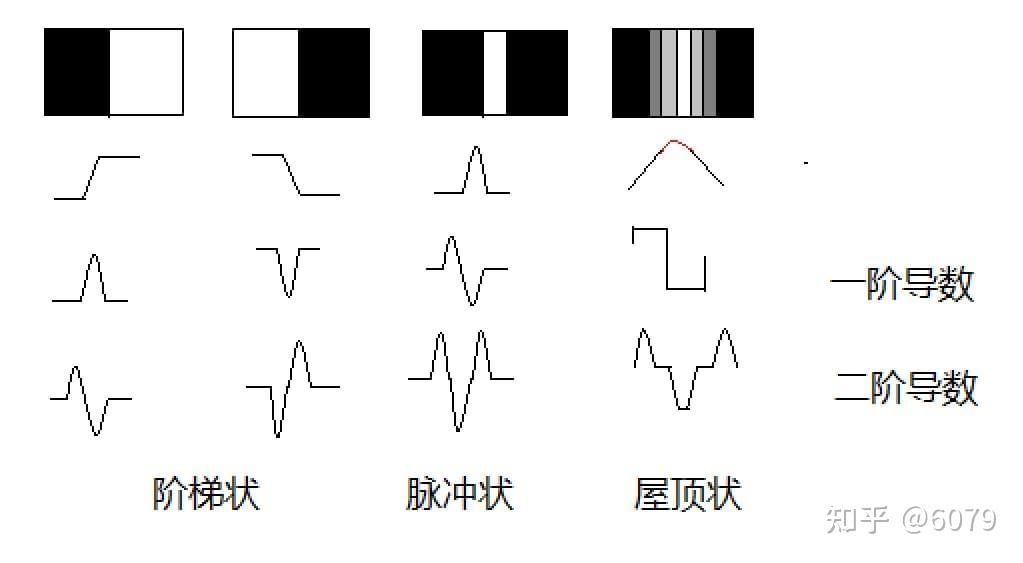
EASU 主要是解决阶梯状边缘，因此特征约接近阶梯状边缘，对应的 $\omega$ 应该越小，即当 $x \in [1,2]$ 时 $L(x)$ 返回的权重小于 0，同时对应像素 $Q$ 计算上下左右方向上的像素点，定义特征 $F$ 的计算公式（这里 $f(x)$ 获得做过灰度化处理后的颜色值）：

// Simplest multi-channel approximate luma possible (luma times 2, in 2 FMA/MAD).
float l = b * 0.5 + r * 0.5 + g;

$$
\begin{aligned}
F &= (FX^2 + FY^2) \
FX &= \frac{ |f-d| }{ max(|f-e|, |e-d|) } = \frac{|f(Q_{x+1,y})-f(Q_{x-1,y})|}{max \left( |f(Q_{x,y}) - f(Q_{x-1,y})|, |f(Q_{x+1,y}) - f(Q_{x,y})| \right) } \
FX &= \frac{ |i-b| }{ max(|i-e|, |e-b|) } = \frac{|f(Q_{x,y-1})-f(Q_{x,y+1})|}{max \left( |f(Q_{x,y+1}) - f(Q_{x,y})|, |f(Q_{x,y}) - f(Q_{x,y-1})| \right) }
\end{aligned} \tag{7}
$$

EASU 最后还对 $FX^2$、$FY2$ 的值做了限制，将其限制在 $[0,1]$ 范围内

A_STATIC AF1 ASatF1(AF1 a){return AMinF1(1.0f,AMaxF1(0.0f,a));}
lenX=ASatF1(abs(dirX)*lenX);

最后将 $F$ 的值归一化后，得到 $Feature$ 的计算公式：

$$
Feature = \left( \frac{F}{2} \right)^2 \tag{8}
$$

当像素是边缘的时候，$Feature$ 的值越大，接近 1，反之则越小，趋近于 0

边缘特征 $Feature$ 跟变量 $\omega$

前面我们已经找到了区分边缘的特征值 $Feature$，以及可以通过 $\omega$ 调整区间 $[1,2]$ 取值范围的拟合曲线了（公式 6），接下来就是要建立 $Feature$ 跟 $\omega$ 之间的联系。

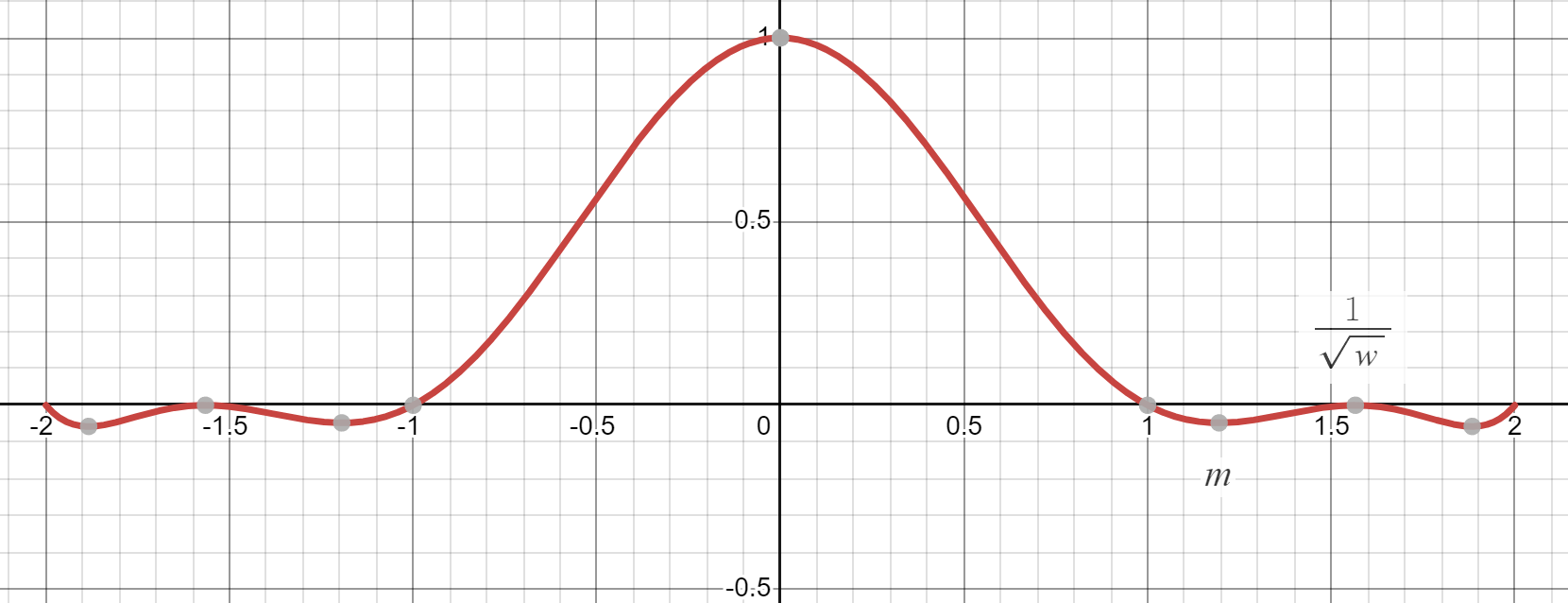
公式 6 中的函数 $L(x), x \in [-2,2]$ 是关于 $y$ 轴对称的，因此这里只分析正半轴（事实上，EASU 里也只用到了正半轴），在正半轴上 $L(x)$ 有三个根：$x=1;x=2;x=\frac{ 1 }{ \sqrt {\omega} }, (\omega > 0)$。

当 $\frac{1}{ \sqrt{\omega} } \in [1,2]$ 时（$\omega \in [\frac{1}{4}, 1]$），区间 $[1, \frac{1}{ \sqrt{\omega} }]$ 中有一个极小值 $m$。

$\frac{1}{ \sqrt{\omega} } \rightarrow 1$ : $m \rightarrow 0$
$\frac{1}{ \sqrt{\omega} } \rightarrow 2$ : $m \rightarrow -\frac{2187}{16483}$

注意到当 $\frac{1}{ \sqrt{\omega} } \in [1,2]$ 时， $x \in [ \frac{1}{ \sqrt{\omega} }, 2]$ 区间出现了一个负的 Lobe 部分，为了解决这个问题，EASU 进行了截断，只取 $x \in [0, \frac{1}{ \sqrt{\omega} }]$ 区间。

因此可以通过改变 $\frac{1}{ \sqrt{\omega} }$ 的值来控制 $[1, \frac{1}{ \sqrt{\omega} }]$ 区间里负值的大小（用来做公式 4 中的负权重）。

$$
\omega = 1 - \frac{3}{4}Feature \tag{9}
$$

但是由于 $\frac{1}{ \sqrt{\omega} }$ 在趋近于 $1$ 时，负权重不够，会导致边缘信息识别不够，因此 EASU 将 $\frac{1}{ \sqrt{\omega} }$ 的范围限定在 $[\sqrt{2}, 2]$，因此 $\omega \in [\frac{1}{4}, \frac{1}{2}]$，得出新的线性关系：

$$
\omega = \frac{1}{2} - \frac{1}{4}Feature \tag{10}
$$

下面是拟合曲线根据 $Feature$ 变化图像：

ESAU 同时限定了 $x$ 的范围为 $x \in [0, \frac{1}{\sqrt{\omega}} ]$，即 $x = min(x, \frac{1}{\sqrt{\omega}} )$

$Feature$ 获得

EASU 计算 $Q$ 点特征时，因为最终算出来的 $Q$ 不一定是整数，因此采用的是采样像素点 $Q$ 周围 12 个像素的值来计算，首先 EASU 进行 12 次采样，分别获取像素 $Q$ 周围点的像素值：

上图中的 $f$ 是对应超采前的像素点 $Q$
每次使用 Gather4 指令批量采样 4 个像素点中的一个通道，例如浅绿色框采样的顺序是 ijfe，因为像素有三个通道 RGB，因此最终是 4 * 3 次采样（z 表示多余的像素，计算时不会用到）。

然后，计算特征时，分四组分别计算出 4 个 $Feature$

然后再使用双线性插值得到最终 $Feature$，如下图所示 $O = floor(Q)$，$u$、$v$ 则是 $Q$ 到 $O$ 的偏移。

$$
Feature = (1-u)(1-v)f_1 + u(1-v)f_2 + uvf_3 + (1-u)vf_4 \tag{11}
$$

梯度

计算 $Feature$ 的同时，EASU 还计算了 $Q$ 点的像素灰度变化的梯度（灰度值变化最快的方向），同样也是分 4 组计算梯度，最后双线性插值得出最终的梯度向量。

$$
\begin{aligned}
D_x &= f - d = f(Q_{x+1, y}) - f(Q_{x-1, y}) \
D_y &= i - b = f(Q_{x, y+1}) - f(Q_{x, y-1})
\end{aligned} \tag{12}
$$

$\vec{D} = (cos\theta, sin\theta)$，其中 $\theta$ 是梯度向量角度

采样颜色值

到这里我们得到了像素 $Q$ 的梯度，以及 $Feature$，然后分别对 $Q$ 周围的 12 个采样点，按照梯度角度进行旋转（这部分是个人理解，希望有大佬能指点一下，因为边缘不一定是水平方向上的边缘，会按照梯度来，但是我们可以按照梯度旋转后，将边缘旋转到阶梯状边缘，EASU 这里选择的是旋转采样核）。

上图展示的 $\vec{D} = (cos45 ^{\circ}, sin45 ^{\circ})$ （红色箭头）下的情况，注意 $x$、$y$ 轴的正方向，旋转是按照向量原点，顺时针旋转 $\theta$ 角度。

如上图，采样点 $b$ 跟 $Q$ 之间的向量 $\vec{QB}$ 按照梯度旋转：

$$
\begin{aligned}
x_r &= x_{QB} * cos\theta + y_{QB} * sin \theta \
y_r &= -x_{QB} * sin \theta + y_{QB} * cos \theta
\end{aligned} \tag{13}
$$

旋转完毕后，采样核不再是中心对称了，因此 EASU 定义了一个将旋转向量根据梯度和 边缘特征 进行缩放的公式：

$$
\begin{aligned}
Stretch &= \frac{ 1 }{ max(|sin\theta|, |cos\theta|) } \
S_x &= 1 + (Stretch - 1) * Feature \
S_y &= 1 - 0.5 * Feature
\end{aligned} \tag{14}
$$

然后得出 $QB$ 旋转缩放后向量坐标:

$$
\begin{aligned}
S_{xb} = x_r * S_x \
S_{yb} = y_r * S_y \
\end{aligned} \tag{15}
$$

最后求出向量的模：

$$
d_b = min( \sqrt{S_{xb}^2 + S_{yb}^2}, \frac{ 1 }{ \sqrt{\omega} } ) \tag{16}
$$

将得出的 $d_b$ 带入到公式 6，求出 $b$ 像素点的权重值

这里使用了采样点 $Q_i$ 到 $Q$ 的欧式距离来应用之前的权重公式
$$
L(x) = \left[\frac{25}{16}\left( \frac{2}{5} x^2 - 1 \right)^2 - \left( \frac{25}{16} - 1 \right) \right](\omega x^2 - 1)^2 \tag{6}
$$

其他像素点依次按照这样的方法求出对应像素的权重值，最后利用公式 4，即可求出上采样 $P$ 点的像素值。

$$
f(P) = \frac{\sum_i f(Q_i)H(Q_i)}{\sum_i H(Q_i)} \tag{4}
$$

EASU 里最后会对求出的颜色做限制，限制颜色的最大最小值只能在这 12 个采样点颜色之间，据说可以减少 ringing 效果。

/// aw 是公式 4 的分子
/// ac 是公式 4 的分母的倒数
/// min4 max4 是 12 个采样点的最小最大颜色值（RGB）
pix=min(max4,max(min4,aC*AF3_(ARcpF1(aW))));

总结

总结一下，EASU 阶段其实就是根据像素灰度，计算得到 $Feature$，然后得到 $\omega$，用来调整拟合曲线的窗口

当像素越接近边缘像素时：拟合函数返回负权重，用来提取边缘，锐化效果强
当像素越接近非边缘像素时：拟合函数返回正数，用来平滑非边缘像素

RCAS（Robust Contrast Adaptive Sharpening）

上采样结束后，FSR 最后对上采样得到的图像进行一次 RCAS （在 CAS 基础进行改进）的锐化处理，将边缘的信息进一步强化，RCAS 其实是拉普拉斯算子的变种：

则最后像素 $P$ 按照上面的算子进行加权计算即可：

$$
F(P) = \frac{ f(P) + w * ( f(P_{x-1,y}) + f(P_{x+1,y}) + f(P_{x,y-1}) + f(P_{x,y+1}) ) }{4\omega + 1} \tag{17}
$$

这里需要从已经超分后的图像上进行采样颜色，需要采样 5 个点的像素值

对于 $\omega$ 权重，RCAS 计算方法是获取像素 $P$ 点周围四个像素的值来计算，先求出这 5 个像素的最大值 MAX，最小值 MIN，这里也是用到是颜色值来计算。

$$
\omega = max \left( -\frac{Min}{4Max}, \frac{ 1-Max }{ 4Min - 4 } \right) * Scale \tag{18}
$$

$Scale$ 为采样之后分辨率跟原分辨率的比值。

RCAS 中为了确保 $\omega$ 为负数，最后对 $\omega$ 做了限制：

$$
\omega = max \left( -\left(\frac{1}{4} - \frac{1}{16} \right), min (\omega, 0) \right)
$$

对于每个通道 $RGB$ 都计算一次对应的 $w_R$、$w_G$、 $w_B$

原图	双线性插值	FSR

下面是 双线性插值 跟 FSR 的对比效果：

这里写了个 python 版的 FSR 来测试对比结果。

后续

FSR 1.0

EASU 阶段采样 12 像素，耗时比较多，KM 上介绍了一个种 5-Tap ⁴ 的 Lanczos2 的卷积，可以减少 EASU 阶段的开销，当然效果上也会有一些些打折。

FSR 2.0

FSR 2.0 增加了时域上的缩放算法，会使用上一帧的数据， FSR 2.0 效果更细腻，自带 TSAA，但是开销非常大，建议在 PC 平台上使用 FSR 2.0，设备推荐使用 FSR 1.0，后续会研究下 FSR 2.0。

参考

1.详细剖析 AMD FSR 算法

2.FidelityFX-FSR 官方文档

3.FidelityFX-FSR 源码

4.图像处理学习笔记（十四）——图像边缘锐化的基本方法(理论篇)

5.Bicubic Filtering in Fewer Taps